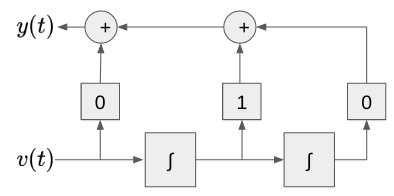
...

[SS] Differential Equation : 2nd Canonical Form

다음과 같은 미분 방정식을 2nd canonical form으로 표현. $$\begin{aligned}(D^2+3D+2) y(t) &= D x(t)\end{aligned}$$ $D$ : 미분연산자. 우선 적분기를 사용하기 위해 미분연산자를 제거. $$D^{-2}[(D^2+3D+2) y(t)] = D^{-2}[D x(t)] \\ (1+3D^{-1}+2D^{-2}) y(t) = D^{-1} x(t)$$ 중간변수 $v(t)$를 도입. $$(1+3D^{-1}+2D^{-2}) y(t) = D^{-1} x(t) \\ y(t)=\frac{D^{-1}}{1+3D^{-1}+2D^{-2}} x(t) \\ y(t) = D^{-1} \frac{x(t)}{1+3D^{-1}+2D^{-2}} \\ y(t) = D^{-1} v(t)..

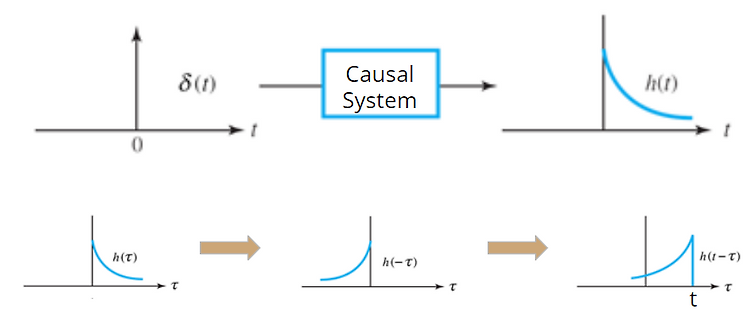
[SS] Causal LTI System and Convolution

LTI system이 causal인 경우, impulse response $h(\tau)$는 $\taut$일 때 값이 0임. 때문에 Causal LTI System의 출력을 구하는 Convolution의 범위는 $(-\infty, \infty)$를 모두 처리할 필요 없음. 즉, $h(\tau)$와 $x(t-\tau)$의 곱이 값을 가지는 영역만 고려하면 된다.

[SS] Convolution Example : Pulse Function

Pulse function $f(t)$ (blue)와 $g(t)$ (red)의 convolution을 보여주는 gif임. $g(t)$를 reflection시킨 후 slide을 시킴. 검은색 라인이 바로 $(f*g)(t)$의 결과를 보여줌. 둘다 unit pulse이므로 convolution의 결과는 노란색으로 표기된 겹치는 부분의 넓이가 됨. $$(f*g)(t) = \int^\infty_{-\infty} f(\tau) g(t-\tau) d\tau$$ 1. $t=-1$ 일 때 겹치기 시작하므로 이후 $(f*g)(t)$의 값이 0 보다 커짐. 2. $t=0$ 일 때 $g(t-\tau)$와 $f(\tau)$가 정확히 일치하므로 가장 큰 $(f*g)(t)$의 값을 가짐. 3. 이후 겹치는 영역이 줄어들므로 $(..

[SS] Convolution Op.에서 교환법칙 증명.

$$\begin{aligned}y(t)&=x(t)*h(t)\\&=\int^\infty_{-\infty}x(\tau)h(t-\tau)d\tau \\ &=- \int^{-\infty}_\infty x(t-l)h(l) dl \quad\quad \leftarrow l=t-\tau \\ &=- \int^{-\infty}_\infty h(l) x(t-l)dl \\&=\int^{\infty}_{-\infty} h(l) x(t-l)dl\\&=\int^{\infty}_{-\infty} h(l) x(t-l)dl \quad\quad \leftarrow l\text{을 }\tau\text{로 표기 변경} \\ &=\int^{\infty}_{-\infty} h(\tau) x(t-\tau)d\tau \\&=h(t)*x(t)\en..

[SS] Output of LTI System : Convolution with Impulse Response

LTI System $T$를 다음과 같은 수식으로 나타낼 수 있다고 하자.$$y(t) = T\left\{x(t)\right\}$$where$x(t)$ : input signal에 해당하는 function.$y(t)$ : output signal에 해당하는 function.여기서,sifting property에 의해 impulse function들의 weighted sum으로 $x(t)$를 다음과 같이 나타낼 수 있다.$$x(t)=\int^\infty_{-\infty}x(\tau)\delta(t-\tau)d\tau$$2023.08.21 - [.../Signals and Systems] - [SS] Properties of Impulse Function [SS] Properties of Impulse Fun..

[SS] System의 종류 (3)

Dynamic Systems and Instantaneous Systems https://bme808.blogspot.com/2022/10/dynamic-system.html SS : Dynamical Systems and Instantaneous Systems Dynamical System 특정 시간 $t$에서 System의 출력이 $t$이전의 과거의 입력과 출력에 영향을 받는 경우 , 해당 시스템을 dynamical system이라고 부름. Dynamical System (or Dynamic S... bme808.blogspot.com Lumped parameter system vs. distributed parameter system Lumped parameter system 구성 요소의 물리적 특..

[SS] System의 종류 (2) : Time Invariant, Causal

Time Invariant System and Time Varying System $$y(t-t_0) = T\left\{ x(t-t_0) \right\}$$ 시스템 특성(parameters)이 시간에 따라 불변(invariant) 시간에 상관없이 같은 입력에 대해서는 같은 반응을 나타냄 시불변이 아닌 시스템을 시변(time varying) 시스템이라고 한다. 가장 많이 모델링 및 분석되는 기본적인 system은 linear time-invariant system (LTI System)이기 때문에 Time Invariant System에 대한 확실한 이해가 중요함. 커피자판기는 time invariant system인가? Causal System and Non-causal System Causal Syst..

[SS] System의 종류 (1) : Continuous, Linear

1. Continuous System & Discrete SystemContinuous System입력과 출력이 연속 신호인 시스템Discrete System입력과 출력이 이산 신호인 시스템2. Linear System & Non-linear systemLinear system $\mathcal{T}\left\{ \quad \right\}$은 다음 두가지 property를 가짐.Additivity (가산성) property$$\begin{matrix} y_1(t)=\mathcal{T}\left\{x_1(t)\right\} \\ y_2(t)=\mathcal{T}\left\{x_2(t)\right\}\end{matrix} \Rightarrow \mathcal{T}\left\{x_1(t)+x_2(t)\righ..

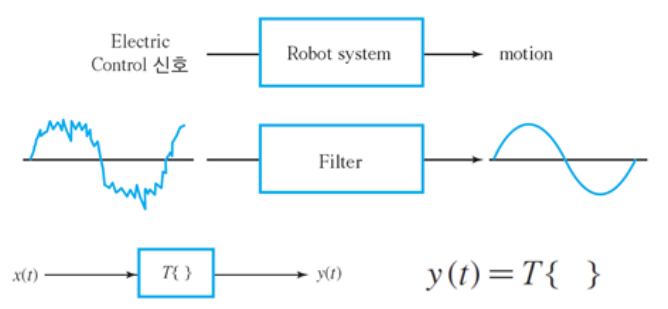
[SS] System 이란?

System이란 하나의 신호를 다른 신호로 매핑(mapping) 또는 변형(transform)하는 규칙 function of functions, transformation of functions 일련의 신호(입력)를 특정한 목적에 맞도록 조작하고 처리(교환, 변환, 가공, 추출, 전송)해 다른 일련의 신호(출력)를 만드는 실체(장치) System Description에 필요한 요소들 input output (or response) 동작규칙 위의 3가지 요소에 의해 명확하게 기술됨. 주로 수학적 표현 (equation, 방정식)이 사용됨. System modeling도 System description과 유사 (modeling의 결과물이 system description으로 나오는 경우가 대다수) Syst..

[SS] Properties of Impulse Function

Impulse function (or Dirac delta function)은 이상적으로, 오직 한 점에서만 무한대의 값을 가지고,나머지에서는 0의 값을 가지며,적분시 면적인 1이 되는 함수다른 function을 분석하거나, system의 response를 측정할 때, Basis Function으로 사용됨.어떤 continuous function도 impulse function의 weighted sum으로 표현됨.Derivative (도함수) of Unit Step FunctionImpulse function은 unit step function의 derivative(도함수)라고 볼 수 있음. 유도.impulse function을 적분하면 다음이 성립함.$$\int^t_{\tau=-\infty} \delt..