728x90
728x90
Causal LTI System에서의 Convolution
LTI system이 causal인 경우,
- impulse response $h(\tau)$는 $\tau<0$ 일 때 값이 0임.
- shifted reflected response $h(t-\tau)$는 $\tau>t$일 때 값이 0임.
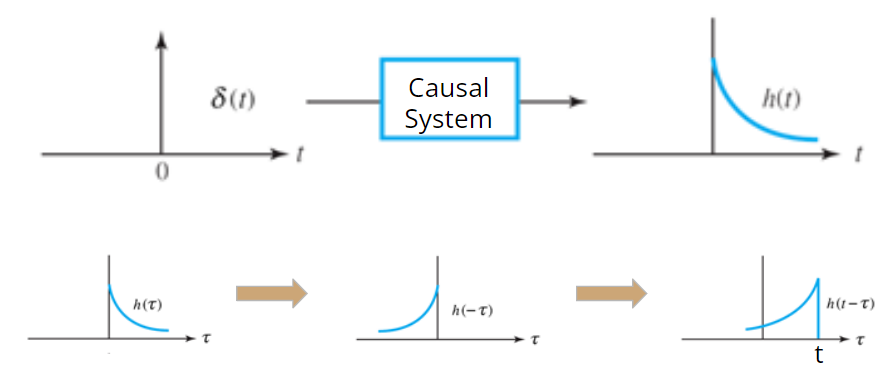
때문에 Causal LTI System의 출력을 구하는 Convolution의 범위는 $(-\infty, \infty)$를 모두 처리할 필요 없음.

즉, $h(\tau)$와 $x(t-\tau)$의 곱이 값을 가지는 영역만 고려하면 된다.
728x90
'... > Signals and Systems' 카테고리의 다른 글
| [SS] RLC Circuit & Differential Eq (0) | 2023.08.22 |
|---|---|
| [SS] Differential Equation : 2nd Canonical Form (0) | 2023.08.22 |
| [SS] Convolution Example : Pulse Function (0) | 2023.08.22 |
| [SS] Convolution Op.에서 교환법칙 증명. (0) | 2023.08.21 |
| [SS] Output of LTI System : Convolution with Impulse Response (0) | 2023.08.21 |