728x90

y(t)=x(t)∗h(t)=∫∞−∞x(τ)h(t−τ)dτ=−∫−∞∞x(t−l)h(l)dl←l=t−τ=−∫−∞∞h(l)x(t−l)dl=∫∞−∞h(l)x(t−l)dl=∫∞−∞h(l)x(t−l)dl←l을 τ로 표기 변경=∫∞−∞h(τ)x(t−τ)dτ=h(t)∗x(t)
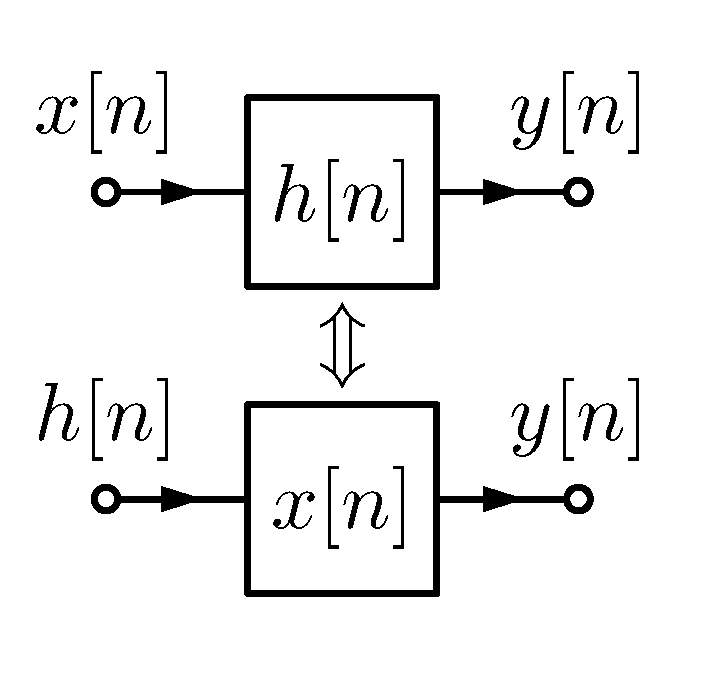
input function과 impulse response를 바꾸어서
처리해도 같은 출력을 구할 수 있음을 유의할 것.
반응형
'... > Signals and Systems' 카테고리의 다른 글
| [SS] Causal LTI System and Convolution (0) | 2023.08.22 |
|---|---|
| [SS] Convolution Example : Pulse Function (0) | 2023.08.22 |
| [SS] Output of LTI System : Convolution with Impulse Response (0) | 2023.08.21 |
| [SS] System의 종류 (3) (0) | 2023.08.21 |
| [SS] System의 종류 (2) : Time Invariant, Causal (0) | 2023.08.21 |