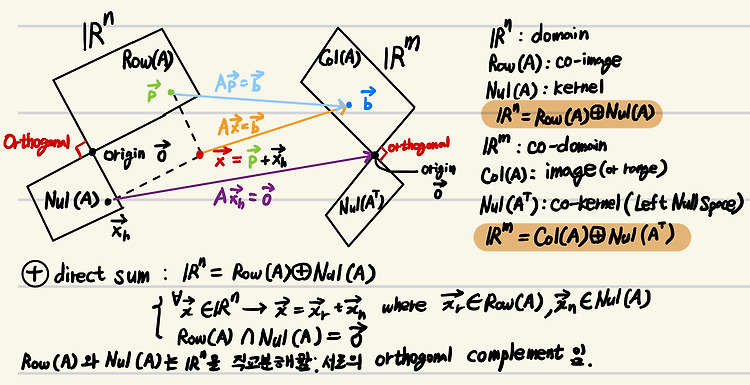
[LA] A $\mathbf{x}=\mathbf{b}$ 에서의 4개의 Subspace 와 Complete Solution
·
.../Linear Algebra
$A\mathbf{x} = \mathbf{b}$와 4개의 Fundamental Subspaces$A\mathbf{x} = \mathbf{b}$ 는 Linear System을 나타내는 Matrix Equation이면서, $\mathbb{R}^n$에서 $\mathbb{R}^m$으로의 Linear Transform을 나타냄.여기에서 4개의 중요한 Subspace 가 존재하며, 이를 이해하면 consistent에 대한 보다 깊은 이해 및 선형변환에서의 domain과 image등을 vector space로 파악할 수 있게 됨.0. Prerequisites더보기2024.10.28 - [.../Math] - [Math] Basis [Math] Basis기저(Basis)는 vector space (또는 function..




