$A\mathbf{x} = \mathbf{b}$와 4개의 Fundamental Subspaces
$A\mathbf{x} = \mathbf{b}$ 는 Linear System을 나타내는 Matrix Equation이면서, $\mathbb{R}^n$에서 $\mathbb{R}^m$으로의 Linear Transform을 나타냄.
여기에서 4개의 중요한 Subspace 가 존재하며, 이를 이해하면 consistent에 대한 보다 깊은 이해 및 선형변환에서의 domain과 image등을 vector space로 파악할 수 있게 됨.
0. Prerequisites
2024.10.28 - [.../Math] - [Math] Basis
[Math] Basis
기저(Basis)는 vector space (또는 function space) 에서 모든 요소(Element)를 나타내기 위해 필요한 최소한의 (선형)독립적인 요소 집합(vector set or function set).Basis (기저)는 벡터 공간 (또는 함수 공간)의 구
dsaint31.tistory.com
2024.05.29 - [.../Linear Algebra] - [LA] Span (생성)
[LA] Span (생성)
Span주어진 Vector들 (=Vector set)에 대한 Span은해당 vector들의 Linear Combination을모두 포함하고 있는 Vector Set을 의미한다.참고로, 위의 정의에서 Linear Combination을 Affine Combination으로 바꾸면, Affine Hull(or A
dsaint31.tistory.com
2022.04.05 - [.../Math] - [Math] Definition of Vector Space and Sub-Space
[Math] Definition of Vector Space and Sub-Space
Vector 의 엄밀한(?) 정의는 Vector Space의 Element임.즉, Vector를 제대로 이해하려면 Vector Space에 대한 정의를 확실히 이해해야 한다.Vector Space의 정의.Vector Space는 아래를 만족하는 Non-Empty Set을 가르킴.Ve
dsaint31.tistory.com
2022.10.07 - [.../Math] - [LA] Basis of Column Space and Pivot Columns
[LA] Basis of Column Space and Pivot Columns
Basis of Column Space and Pivot Columns행렬 $A$의 Pivot column들은 $A$의 column space $\text{Col }A$의 basis를 이룸.pivot column은 $A\textbf{x}=\textbf{b}$의 linear system(선형 연립방정식)의 관점에서 basic variable에 해당!
dsaint31.tistory.com
2024.07.08 - [.../Linear Algebra] - [LA] Null Space
[LA] Null Space
Null Space는 주로 matrix 에 관련된 맥락에서 사용되며,Linear Transformer의 맥락에서는 Kernel이라고 불림.Definition : Null SpaceThe null space of an $m \times n$ matrix $A$, written as Nul $A$, is the set of all solutions of the hom
dsaint31.tistory.com
2024.07.08 - [.../Linear Algebra] - [LA] Rank: Matrix의 속성
[LA] Rank: Matrix의 속성
Definition: Rank ◁ matrix 속성The rank of a matrix $A$, denoted by rank $A$,is the dimension of the column space of $A$.Matrix를 이루는 Column Vectors에서 Linearly Independent 인 것들의 수를 의미Row Space의 Dimension 의 경우를 강
dsaint31.tistory.com
1. Four Fundanmental Subspace
다음은 이를 설명하는 간단한 그림임.
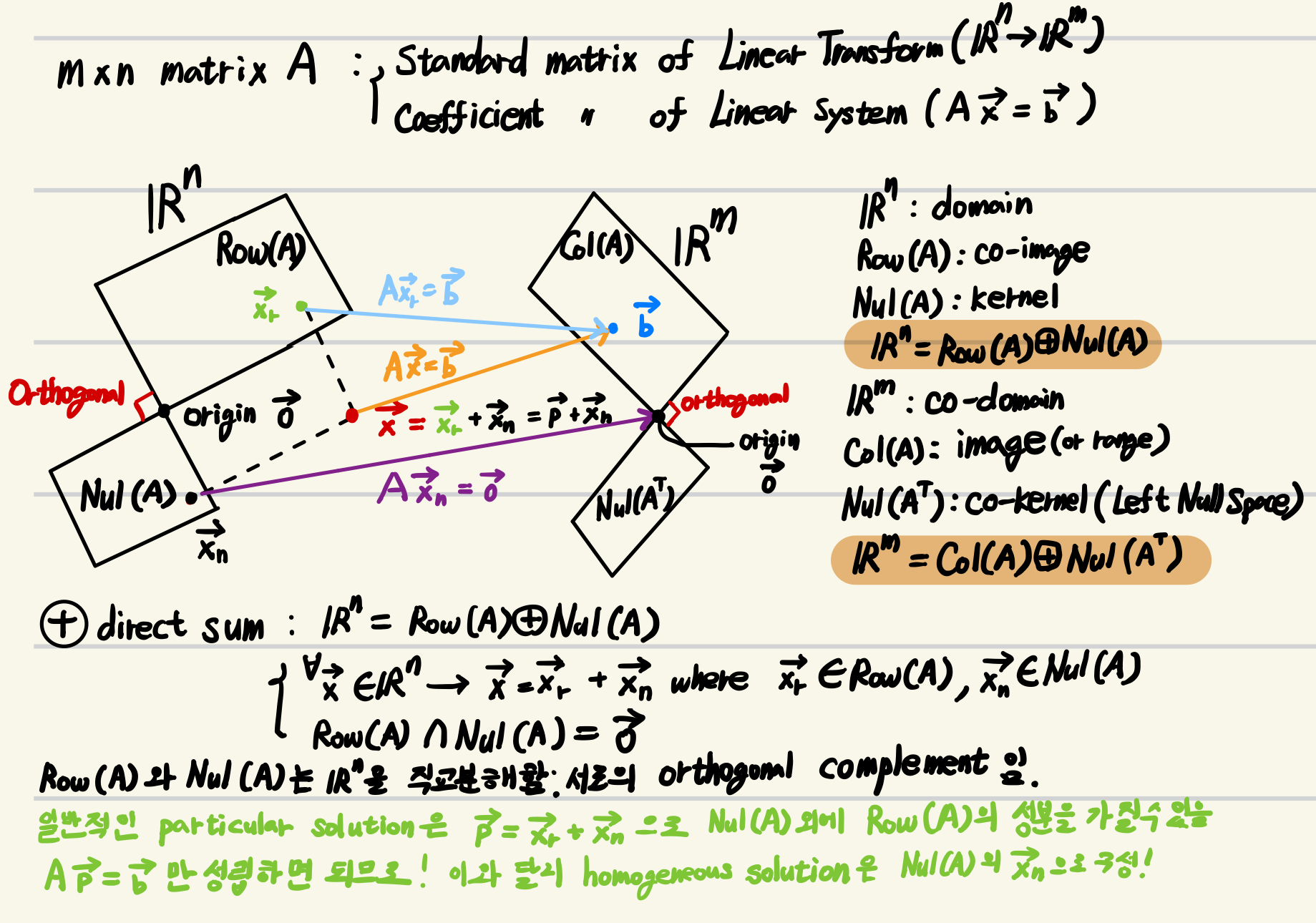
- $\mathbf{p}$: Particular Solution, $A\mathbf{p}=\mathbf{b}$를 만족하는 특정해.
- $\mathbf{x}_r \in \text{Row}(A)$: Row space의 벡터로 particular solution을 통해 얻어짐.
- $\mathbf{x}_n \in \text{Nul}(A)$: Null space의 벡터로, homogeneous solution을 통해 얻어짐.
Rank Theorem (or Rank-Nullity Theorem)에 따라 다음이 성립
$$
\dim(\text{Col}(A))+ \text{Nullity}(A) = n \\
\dim(\text{Row}(A))+ \text{Nullity}(A) = n \\
\text{rank}(A)=\dim(\text{Col}(A))=\dim(\text{Row}(A))
$$
다음도 성립함.
$$
\dim(\text{Row}(A))+ \text{Nullity}(A^\top) = m
$$
1-1. 4개의 기본 부분공간(Fundamental Subspaces)
Matrix $A$와 관련된 4개의 Fundamental Subspace들은 다음과 같음:
- Column Space $\text{Col}(A)$ ) — Column Space of $A$
- $A$를 standard matrix로 가지는 Linear Transform의 image (or range)임.
- $A$의 Column Vectors가 span하는 vector space.
- 가능한 모든 $A\textbf{x}$의 결과가 포함된 공간 (or set)
- $A\mathbf{x} = \mathbf{b}$가 consistent하기 위한 필요충분조건은 $\mathbf{b} \in \text{Col}(A)$임.
- 이 공간의 차원은 rank($A$)에 해당.
- Row Space $\text{Row}(A)$ — Row Space of $A$:
- $A$를 standard matrix로 가지는 Linear Transform의 Coimage임.
- $A$의 row vectors가 span하는 vector space.
- 이는 $\text{Col}(A^\top)$와 동일.
- Row space의 차원(=rank($A$))은 Column space와 동일
- 즉 $\dim(\text{Row}(A)) = \dim(\text{Col}(A))$
- Null Space $\text{Nul}(A)$ — Null Space of $A$
- $A\mathbf{x} = \mathbf{0}$을 만족하는 모든 $\mathbf{x}$들의 vector space.
- 즉, $A$가 $\mathbf{0}$으로 보내는 모든 벡터들의 집합.
- 동차방정식(homogeneous equation) $A\mathbf{x} = \mathbf{0}$의 Solution Space (or Solution Set).
- $\text{Nul}(A)$의 차원은 nullity(A) 라고 기술되며, free variable이 존재할 경우 이 차원이 0보다 커짐: 무수히 많은 solution 존재.
- Kernel이라고도 불림.
- Left Null Space $\text{Nul}(A^\top)$ — Left Null Space of $A$
- Co-kernel이라고도 불림.
- $A^\top \mathbf{y} = \mathbf{0}$을 만족하는 $\mathbf{y}$들의 vector space.
1-2. $A\mathbf{x} = \mathbf{b}$의 solution의 갯수
- $A$ 가 full column rank인 경우
- ($A$의 rank와 column의 수가 같음)
- solution은 기껏해야 1개 존재: (없기 쉬움)
- $\textbf{b}$가 매우 높은 차원 $\mathbb{R}^m$에 속하는 vector인데, 이것이 보다 낮은 차원의 $\text{Col}A$로 표현 가능해야만 solution이 존재할 수 있는 상황.
- 거의 solution이 없기 쉬운 경우임.
- nullity of $A$는 0
- $A$가 full row rank인 경우
- solution이 무한하게 존재함.
- homogeneous solution 이 무수히 많이 존재.
- $\textbf{b}$가 매우 낮은 차원 $\mathbb{R}^m$에 속하는 vector이므로, 이것이 훨씬 높은 차원의 $\text{Col}(A)$에서 이를 표현하기가 매우 쉽기 때문에 무한히 많은 solution이 존재.
- $\textbf{x}_h$이 무수히 많이 존재
- nullity of $A$ 가 0이 아님.
- $A$가 full rank인 경우. ($A$가 square matrix) :
- unique solution $\textbf{x}=A^{-1}\textbf{b}$.
- 참고로, square matrix에서 rank deficient이면 해가 없음!
- nullity of $A$가 0
- $A$가 rank deficient 인 경우.
- solution이 무한히 존재하거나,
- $\textbf{b}$가 column space에 존재할 경우 무한히 존재.
- solution이 존재하지 않음: inconsistent
- nullity of $A$가 0이 아님.
- solution이 무한히 존재하거나,
1-3. 일관성(Consistency) 조건
- $\mathbf{b}$가 열공간(Column Space $\text{Col}(A)$에 속해야 함: $n > m$인 경우 보다 확률이 높아짐 (무한히 많은 solution. 미지수보다 식이 적게 주어진 연립방정식)!
- 즉, $A\mathbf{x} = \mathbf{b}$의 해가 존재하려면 $\mathbf{b}$가 $A$의 열벡터들의 선형 결합으로 표현될 수 있어야 함.
2. Complete Solution = Particular Solution + Homogeneous Solution
$A\mathbf{x} = \mathbf{b}$의 완전해(complete solution)는 두 가지 성분으로 구성됨
$$
\mathbf{x} = \mathbf{p} + \mathbf{x}_h
$$

- $\mathbf{p}$: 특정해(Particular Solution)
- $A\mathbf{x} = \mathbf{b}$를 만족하는 하나의 특정한 해.
- 특정해 $\mathbf{p} \in \mathbb{R}^n$는 linear transform $A$를 통해 $\text{Col}(A)$에 포함된 벡터 $\mathbf{b} \in \mathbf{R}^m$로 변환됨.
- $\text{Nul}(A)$를 $\mathbf{p}$로 translation하면
- $A\mathbf{x}=\mathbf{b}$의 solution space(=일종의 hyper plane)를 구할 수 있음.
- Complete solution의 차원은 Null Space $\text{Nul}(A)$의 차원과 같음.
- 만약 $A\mathbf{x} = \mathbf{b}$의 해가 존재한다면, 적어도 하나의 특정해 $\mathbf{p}$를 찾을 수 있음.
- $\mathbf{x}_h$: 동차해(Homogeneous Solution)
- 동차방정식 $A\mathbf{x}=\mathbf{0}$의 해 집합에서 선택된 벡터.
- 널공간(Null Space, $\text{Nul}(A)$)에 속하며, 이는 $A\mathbf{x} = \mathbf{b}$의 해가 존재할 경우 자유롭게 추가할 수 있는 성분을 의미.
- 자유롭게 추가가 가능하므로, 만약 nullity of $A$가 0보다 크다면, 무한히 많은 해가 존재하게 됨.
이 것이 바로 공학수학에서 배우는 미분방정식의 해에 대한 선형대수적(or 기하학적)인 해석임!
'... > Linear Algebra' 카테고리의 다른 글
| [LA] Coordinate Mapping (0) | 2025.02.10 |
|---|---|
| [LA] Isomorphism (동형사상) (0) | 2025.02.07 |
| [LA] LDU Decomposition (or LDU Factorization) (1) | 2025.02.05 |
| [LA] 예제: Eigenvalue, Eigenvector 구하기 (기초) (0) | 2025.01.28 |
| [LA] Elementary Row Operation Matrix (0) | 2025.01.27 |
