Gram-Schmidt Process는
임의의 Subspace $W$에서
Orthogonal Basis (or Orthogonomal Basis)를 찾는 과정임.
0. Prerequisite
우선 다음을 기억하자
- Basis에 속하는 Vector들로 Span 하면, Subspace $W$ 내의 모든 Vector를 표현가능!
- Basis 에 속하는 모든 Vector들이 서로 서로 Linear Indepedent임
- 만약 한 걸음 더 나아가 Basis의 모든 Vector들이 서로 Orthogonal인 경우, 해당 Basis는 Orthogonal Basis 이 됨.
- 한 걸음 더 나아가 Basis의 모든 Vector 들의 L2-Norm이 1이 되면(unit vector), 해당 Basis는 Orthonormal Basis임.
2024.10.28 - [.../Math] - [Math] Basis
[Math] Basis
기저(Basis)는 vector space (또는 function space) 에서 모든 요소(Element)를 나타내기 위해 필요한 최소한의 (선형)독립적인 요소 집합(vector set or function set).Basis (기저)는 벡터 공간 (또는 함수 공간)의 구
dsaint31.tistory.com
2022.04.05 - [.../Math] - [Math] Definition of Vector Space
[Math] Definition of Vector Space and Sub-Space
Vector 의 엄밀한(?) 정의는 Vector Space의 Element임.즉, Vector를 제대로 이해하려면 Vector Space에 대한 정의를 확실히 이해해야 한다.Vector Space의 정의.Vector Space는 아래를 만족하는 Non-Empty Set을 가르킴.Ve
dsaint31.tistory.com
1. Gram-Schmidt Process
임의의 Subspace $W$는 Basis로 정의가 되기 때문에,
결국 Gram-Schmidt Process는 주어진 Linearly Independent Vector Set (=Basis)를
Orthogonal Vector Set(직교집합)으로 변환시킴.
1-1. Algorithm
주어진 $W$의 Basis (=선형 독립 벡터 집합) ${\mathbf{v}_1, \mathbf{v}_2, \dots, \mathbf{v}_n}$에서,
Gram-Schmidt Process는 다음과 같이 적용되어
새로운 Orthogonal Set ${\mathbf{u}_1, \mathbf{u}_2, \dots, \mathbf{u}_n}$를 생성:
- 첫 번째 벡터를 초기화:
$$\mathbf{u}_1 = \mathbf{v}_1$$
- 두 번째 벡터부터 시작하여 직교화:
$$\mathbf{u}_k = \mathbf{v}_k - \sum_{i=1}^{k-1} \text{proj}_{\mathbf{u}_i}(\mathbf{v}_k)$$
- 여기서
- $\text{proj}_{\mathbf{u}_i}(\mathbf{v}_k)$는 $v_k$가
- $\mathbf{u}_i$ 위로 Orthogonal Projection 된 성분으로
- 다음과 같이 계산됨:
$$\begin{aligned}\text{proj}_{\mathbf{u}_i}(\mathbf{v}_k) &= \frac{\langle \mathbf{v}_k, \mathbf{u}_i \rangle}{\langle \mathbf{u}_i, \mathbf{u}_i \rangle} \mathbf{u}_i \\ &= \frac{ \mathbf{v}_k^\top \mathbf{u}_i}{\| \mathbf{u}_i \|^2}\mathbf{u}_i\end{aligned}$$
2022.05.19 - [.../Math] - [Math] Orthogonal Projection (정사영)
[Math] Orthogonal Projection (정사영)
Projection $\textbf{x}_1$ onto $\textbf{w}$ (vector $\bf{x}$를 vector $\bf{w}$에 투영) 를 수식으로 표현하면 다음과 같음. $$\begin{aligned}\text{proj}_\textbf{w}\textbf{x}&=\dfrac{\bf{x}\cdot\bf{w}}{\bf{w}\cdot\bf{w}}\bf{w}=\dfrac{\bf{x
dsaint31.tistory.com
- $u_k$ 벡터를 계산한 후, 필요하면 Normalization(정규화)하여 Unit Vector(단위 벡터)를 생성:
$$\mathbf{e}_k = \frac{\mathbf{u}_k}{\|\mathbf{u}_k\|}$$
Gram-Schmidt Process는 다음의 정리로 이어짐:
$\{ \mathbf{0} \}$ 가 아닌 임의의 Subspace $W$는
항상 Orthogonal Basis를 가짐!
1-2. Proof
증명은 다음을 참고
https://youtu.be/4xSgl2nkZ5w?si=MQtnrcRspopUp4kD
2. QR Decomposition
QR Decomposition 는 행렬 $A$ 를 두 행렬 $Q$와 $R$의 곱으로 나타내는 방법임.
여기서:
- $Q$ 는 Orthogonal Matrix(직교 행렬) ($Q^\top Q = I$).
- $R$ 은 Upper Triangular Matrix(상삼각 행렬).
2022.11.17 - [.../Math] - [LA] Orthogonal matrix (직교행렬)
[LA] Orthogonal matrix (직교행렬)
Orthogonal MatrixMatrix의 row vector (and column vector)들이자기자신을 제외한 나머지 row vector (and column vector)들과 orthonormal인 square matrix.$$A^{-1}=A^\top \\ A^\top A = I \\ \mathbf{a}_i^\top \mathbf{a}_j = \mathbf{a}_i \cdot \mat
dsaint31.tistory.com
2-1. 정의
주어진 $m \times n$ 행렬 $A$에 대해:
$$A = Q R$$
2-2. QR Decomposition과 Gram-Schmidt의 관계
- Gram-Schmidt Process는 QR Decomposition의 주요 알고리즘 중 하나로 사용됨.
- Gram-Schmidt Process 는 수치해석적으로는 거의 사용되지 않음 (수치적 불안정성 등의 문제를 가짐)
- 하지만, 개념적인 이해가 가장 쉽고, 이에 대한 구현물들의 이론적으로 설명하는 가장 좋은 방법임.
- 즉, 개념적으로는 Gram-Schmidt Process에 의해 구해진다고 봐도 되나,
실제 LANPACK등의 구현은 다른 방식(Householder, Givens 등등)을 취함.
- $A$의 Column Vectors에 대해 Gram-Schmidt를 수행하면:
- $Q$: $A$의 Column Vectors를 Orthogonalization한 직교화한 벡터들을 column으로 가짐
- Unit Vector로 처리하는게 일반적이나 강제적은 아님.
- 가지고 있는 column들이 서로서로에 대해 최소한 orthogonal함 (대부분 orthogonormal 함).
- Complete Form의 경우, 항상 square matrix로 만들어짐: $Rank(A)$ 보다 크거나 같은 rank를 가질 수 있음.
- $R$: Orthgonalization(직교화 과정)에서 계산된 Scalar Coefficient로 구성됨(Upper Triangular Matrix).
- $Q$: $A$의 Column Vectors를 Orthogonalization한 직교화한 벡터들을 column으로 가짐
QR Decomposition에서는
$Q$를 Orthonomal (최소한 Orthogonal) Column Vector를 가지도록 처리함.
2-3. 알고리즘
- 주어진 행렬 $A$의 Column Vectors를 ${\mathbf{a}_1, \mathbf{a}_2, \dots, \mathbf{a}_n}$라고 하자.
- Gram-Schmidt Process를 사용하여 $Q = { \mathbf{q}_1, \mathbf{q}_2, \dots, \mathbf{q}_n] }$ 을 계산.
- $R$ 행렬의 $r_{ij}$는 다음과 같이 구해짐:
$$
r_{ij} =
\begin{cases}
\langle a_j, q_i \rangle & i \leq j \\
0 & i > j
\end{cases}
$$
위의 알고리즘을 수식적으로 표현하면 다음과 같음:
$$\begin{aligned}A&=QR \\ Q^\top A&=Q^\top QR \\ Q^\top A&=IR \\ Q^\top A&=R \\ \quad \\ \therefore R&=Q^\top A\end{aligned} $$
- $Q$는 Orthogonal (or Orthonormal) Basis를 Column으로 가지므로, $Q^\top Q=I$가 됨.
- 각 Column은 서로에 대해 Orthogonal 이므로 자기 자신과 inner product가 될 경우에만 값을 가지고, 나머지는 모조리 0이 됨: 즉, $Q^\top Q$ 등은 Diagonal matrix 가 됨.
- $Q$의 Column들은 Orthonormal Basis를 이룰 경우, 자기자신과의 dot product의 결과는 모두 1임: $Q^\top Q = I$
$Q^\top A$에서 $R$의 Diagnoal ($r_{kk}$)에 Negative인 수가 있을 경우, 대응되는 $Q$의 Column $\mathbf{q}_k$에 -1을 곱해주고, 해당 $r_{kk}$ ~ $r_{kn}$들에 -1을 곱해줌 (해당 대각 성분이 속한 행에 -1을 곱하는 것임.)
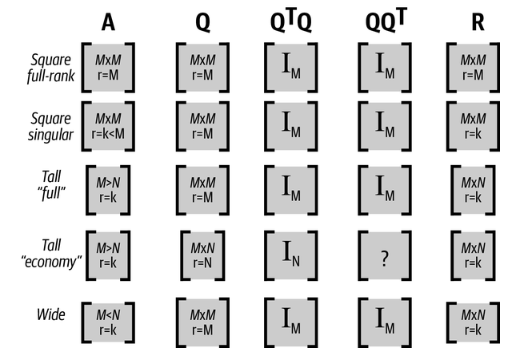
3. QR Decompostion의 종류
앞서 수식적인 표현은 $A$가 (Square) Full Rank인 경우임.
QR Decomposition은 Square Matrix가 아닌 경우에도 적용가능하며, Rank Deficient Matrix인 경우도 적용가능함.
- 만약 $A$가 Full Column Rank Matrix가 아닌 경우, $R$은 완벽한 Upper Triangular Matrix가 아님.
- $\text{Rank} (A)=r$인 경우, $R$의 $r+1$ 행들은 모두 0이 됨.
- $Q$가 항상 Square Matrix로 나오는 경우는 Complete QR Decomposition이고,
Rectangular Matrix가 되는 경우는 Reduced QR Decomposition임.- Complete 의 경우, $Q$는 rank가 $A$보다 크거나 같음: $\mathbb{R}^m$ Span함!
- $R$의 rank가 $A$와 항상 같음.
Complete 인지 Reduced 인지에 따른 각 Matrix의 shape는 다음을 참고:
아래 그림에서 "economy"가 Reduced QR Decomposition을 의미함. (원본: Fig 9-4. Practical Linear Algebra for Data Science, Mike X Cohen, O'Reilly)
다음의 NumPy의 예제들로 $A$에 따른 $Q, R$의 shape를 살펴볼 것.
https://gist.github.com/dsaint31x/9c8b3ac9b7851986b43ab9373dd30d65
LA_QR_Decomposition.ipynb
LA_QR_Decomposition.ipynb. GitHub Gist: instantly share code, notes, and snippets.
gist.github.com
4. QR Decomposition의 활용
1. Linear Equation (특히 Over-determined System)을 푸는데 활용.
$$\begin{aligned} A \mathbf{x} &= \mathbf{b} \\ QR \mathbf{x} &= \mathbf{b} \\ R \mathbf{x} &= Q^\top \mathbf{b}\end{aligned}$$
- $R$은 Upper Triangular Matrix (아니면 그와 비슷한) 이므로 back substitution으로 쉽게 Solution $\mathbf{x}$를 구할 수 있음.
- LR Decomposition보다 수치적으로 안정적.
- Over-Determined System에서 보다 많이 애용됨.
2. Rank 계산에서 유용
- $R$ 에서 Main Diagonal 에서 0이 아닌 갯수를 세면 됨.
3. 직교 기저를 생성하는데 유용: 데이터 정규화 및 직교화.
4. Least Square를 푸는데 유용하게 사용 가능.
- 벡터에 Orthogonal Matrix $Q^\top$ 를 곱할 경우, 벡터의 Euclidean Norm이 보존되는 성질을 이용: $\| Q^\top \mathbf{b}\|_2 = \|\mathbf{b}\|_2$
$$\|A\mathbf{x}-\mathbf{b}\|_2^2 = \|QR\mathbf{x}-\mathbf{b}\|^2_2 = \|Q^\top (QR\mathbf{x} - \mathbf{b}) \|^2_2$$
- 여기서 다음이 성립.
$$Q^\top (QR\mathbf{x}-\mathbf{b}) = Q^\top Q R \mathbf{x} -Q^\top \mathbf{b} = R\mathbf{x}-Q^\top \mathbf{b}$$
- 즉, $\|A\mathbf{x} - \mathbf{b}\|^2_2 = \|R\mathbf{x}-Q^\top \mathbf{b}\|_2^2$으로 식을 바꿀 수 있음.
- 이는 $R\mathbf{x}=Q^\top \mathbf{b}$를 만족하는 $\mathbf{x}$가 최적의 solution을 의미함.
- $R$은 Upper Triangular Matrix (아니면 그와 비슷한) 이므로 back substitution으로 쉽게 $\mathbf{x}$를 구할 수 있음.
같이 보면 좋은 자료들
https://youtu.be/tk6HM0YVL5E?si=Pw7TIWKVUdx2dgAt
https://youtu.be/D7koMV2AeLE?si=4NZWsrF30P5WPDMb
https://youtu.be/KxAX_evOMtw?si=UIF0hR7X_KwFkCTV
2025.01.21 - [.../Linear Algebra] - [Summary] Linear Algebra (작성중)
[Summary] Linear Algebra (작성중)
ML 을 위해 Linear Algebra 공부시 참고할만한 책더보기전체적으로 공부를 한다면 다음을 권함.Linear Algebra and Its Application, 5th ed 이상, David C. Lay5th ed. 는 웹에서 쉽게 pdf도 구할 수 있음.개인적으로 Str
dsaint31.tistory.com
'... > Linear Algebra' 카테고리의 다른 글
| [LA] Elementary Row Operation Matrix (0) | 2025.01.27 |
|---|---|
| [LA] 예제: LU Factorization (or LU Decomposition) 와 Gauss Elimination (0) | 2025.01.27 |
| [LA] Inverse Matrix (0) | 2025.01.25 |
| [LA] Intermediate Matrices for Inverting Full-Rank Matrix: Cramer's Rule (0) | 2025.01.25 |
| [LA] Quadratic Form and Positive/Negative Definite (0) | 2025.01.24 |