differentiation

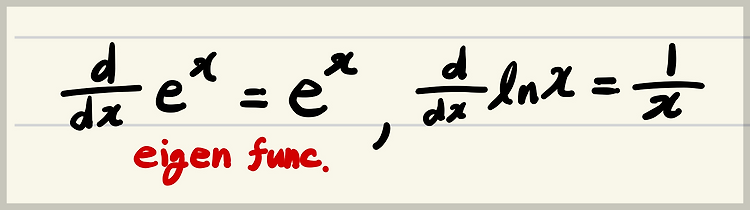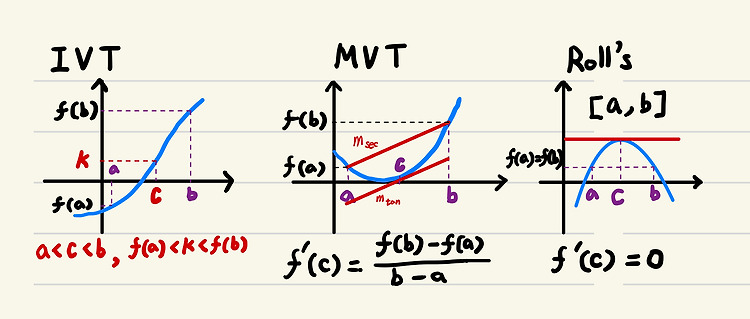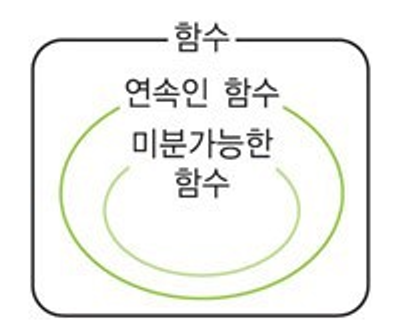
[Math] Continuous 와 Differentiable 의 관계

Differentiable and Continuous Function $f(x)$가 $x=a$에서 미분 가능 ($p$) 하면 $f(x)$는 연속이다($q$). (← implication, 조건명제) $p \implies q$ 는 참(True)이나 이의 역인 $q \implies p$는 거짓(False)임. Example $f(x)=|x|$ : $x=0$에서 continuous하지만 미분가능하지 않음. Differentiable의 조건 (Scalar Function) Function(함수)가 Continuous(연속)이어야 함. 만약 continuous(연속)이라면 좌미분계수와 우미분계수가 같아야 함. $$ \lim_{x \to a^-}\dfrac{f(x)-f(a)}{x-a}=\lim_{x \to a^+}..

[Math] Derivatives of Exponential and Logarithmic Functions

다음이 기본적인 지수와 로그 함수의 도함수임. $$f(x)=e^x \rightarrow f^\prime(x)=e^x$$ $$f(x)=\log x \rightarrow f^\prime(x)=\frac{1}{x} $$ $$f(x)=a^x \rightarrow f^\prime(x)=a^x \log a$$ $$f(x)=\log_a x \rightarrow f^\prime(x)=\frac{1}{x\log a}$$ 2024.02.28 - [.../Math] - [Math] Limits of Log and Exponential Functions [Math] Limits of Log and Exponential Functions 대표적인 경우들은 다음과 같음. $$\underset{x\to 0}{\lim} \frac{..

[Math] The Key Rules of Differentiation

The Key Rules of Differentiation 1. Power rule (다항식의 미분에 핵심) If $f(x)=x^n$, where $n \in \mathbb{R}$, then the derivative of $f$ with respect to $x$ is $f^\prime(x)=nx^{n-1}$. 2. Constant rule if $f(x)=c$ where $c \in \mathbb{R}$ and constant, then the derivative of $f$ with respect to $x$ is $f^\prime (x)=0$. 3. Sum and Difference rule (미분의 선형성) $f$와 $g$ 모두 $x$에 대해 differentiable function이라면, 다..

[Math] Cauch’s Mean Value Theorem

Cauch가 Mean Value Theorem을 일반화시킨 Theorme(정리) : 1821년발표 내용은 다음과 같음. 두 함수 $f(x), g(x)$가 $[a,b]$에서 continuous하고, $(a,b)$에서 differentiable하면, $(a,b)$ 에 다음을 만족하는 $c$가 적어도 하나 존재함. $$(f(b)-f(a))g^\prime (c)=(g(b)-g(a))f^\prime(c)$$ 두개의 함수를 이용하여 derivative와 average ratio of change 간의 관계를 살핌. 증명은 Rolle's Theorem을 이용함. 여기서 $g(x)=x$로 한정할 경우, Mean Value Theorem이 됨 ($g^\prime=1$). $$(f(b)-f(a))=(b-a)f^\prime..

[Math] Intermediate Value Theorem, Mean Value Theorem and Rolle’s Theorem

중간값의 정리(Intermediate Value Theorem, IVT) 와 평균값의 정리(Mean Value Theorem, MVT) 는 미적분학에서 중요한 정리들이며, 서로 유사하게 보이지만 다른 정리임. 중간값의 정리 (Intermediate Value Theorem, IVT) 중간값의 정리는 function의 continuity (연속성)에 대한 Theorem. function $f(x)$가 $[a,b]$에서 continuous이고 $f(a) \ne f(b)$이면, $f(a)$와 $f(b)$ 사이의 어떤 값 $m$에 대해 $f(c)=m$인 $c$가 $(a,b)$에서 적어도 하나 이상 존재. 평균값의 정리 (Mean Value Theorem, MVT) 평균값의 정리는 differtiable func..

[Math] Chain Rule (연쇄법칙)

What is the Chain Rule Chain rule은 composite function에 대한 derivative를 구하는 방법임. $$\displaystyle \frac{d}{dx}\left[f\left(g(x)\right)\right]= f^\prime \left(g(x)\right) g^\prime(x)$$ Chain Rule of Multi-variate Functions $n$-dimensional vector $\bf{x}$의 각 component가 $x_i(t)$라는 scalar function이라면, $\bf{x}$를 input으로 하는 multi-variate function $z=f(\textbf{x})$의 scalar $t$에 대한 ordinary derivative는 다음과..