Cauch가 Mean Value Theorem을 일반화시킨 Theorme(정리) : 1821년발표
내용은 다음과 같음.
두 함수 $f(x), g(x)$가 $[a,b]$에서 continuous하고, $(a,b)$에서 differentiable하면,
$(a,b)$ 에 다음을 만족하는 $c$가 적어도 하나 존재함.
$$(f(b)-f(a))g^\prime (c)=(g(b)-g(a))f^\prime(c)$$
두개의 함수를 이용하여 derivative와 average ratio of change 간의 관계를 살핌.
증명은 Rolle's Theorem을 이용함.
여기서 $g(x)=x$로 한정할 경우, Mean Value Theorem이 됨 ($g^\prime=1$).
$$(f(b)-f(a))=(b-a)f^\prime(c) \\ f^\prime(c)=\frac{f(b)-f(a)}{b-a}$$
2024.02.27 - [.../Math] - [Math] Intermediate Value Theorem, Mean Value Theorem and Rolle’s Theorem
[Math] Intermediate Value Theorem, Mean Value Theorem and Rolle’s Theorem
중간값의 정리(Intermediate Value Theorem, IVT) 와 평균값의 정리(Mean Value Theorem, MVT) 는 미적분학에서 중요한 정리들이며, 서로 유사하게 보이지만 다른 정리임. 중간값의 정리 (Intermediate Value Theorem, IVT)
dsaint31.tistory.com
$g^\prime (x) \ne 0$이라는 조건이 붙을 경우, Rolle's Theorem에 의해 $g(a) \ne g(b)$이므로 다음과 같이 표기할 수 있게됨.
$$ \frac{f^\prime(c)}{g^\prime(c)}=\frac{f(b)-f(a)}{g(b)-g(a)}$$
기하적인 의미는,
$g(t)$와 $f(t)$가 각각 x축과 y축에서 매개변수(parameter), $t$를 공유하는 경우로 생각하면 된다.
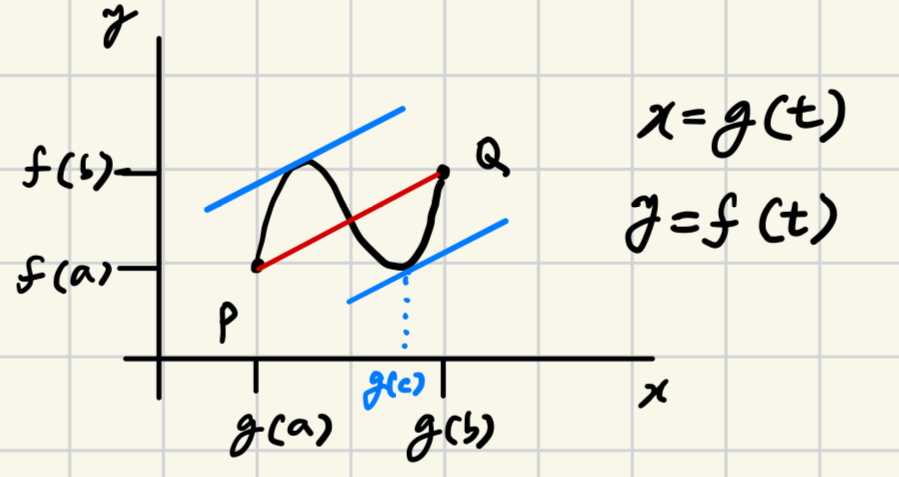
$$\dfrac{dy}{dx}=\dfrac{\frac{df(t)}{dt}}{\frac{dg(t)}{dt}}=\frac{f^\prime(t)}{g^\prime(t)}$$
'... > Math' 카테고리의 다른 글
| [Math] Limits of Log and Exponential Functions (0) | 2024.02.28 |
|---|---|
| [Math] The Key Rules of Differentiation (0) | 2024.02.28 |
| [Math] Intermediate Value Theorem, Mean Value Theorem and Rolle’s Theorem (1) | 2024.02.27 |
| [Math] interval (구간) (0) | 2024.02.27 |
| [Math] Limit of Scalar Function: Left-Sided Limit and Right-Sided Limit (0) | 2024.02.27 |