linear algebra

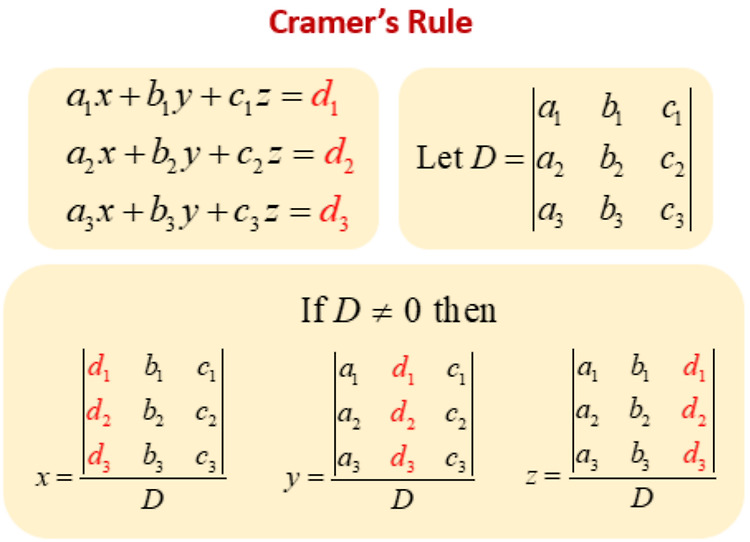
1. Inverse Matrix and Linear SystemLinear Algebra 의 가장 기본적인 응용은 Linear System (선형연립방정식)을 푸는 용도임.다음은 Linear System의 Matrix Equation임. $$A\mathbf{x}=\mathbf{b}$$  Inverse는 이 Linear System의 Solution $\mathbf{x}$를 어찌보면 가장 기본적으로 푸는 방법이라고 볼 수 있음: $$\begin{aligned} A\mathbf{x} &= \mathbf{b} \\ A^{-1}A\mathbf{x} &= A^{-1}\mathbf{b} \\ I \mathbf{x} &= A^{-1}\mathbf{b} \\ \mathbf{x} &= A^{-1}\mathbf{b} \end..

Square Full-Rank Matrix의 Inverse를 Cramer's rule에 기반하여 구하는 방식은 실제 inverse를 구하는 용도로는 많이 사용되지는 않는다.재귀적 방식인지라, 대상이 되는 Square Matrix의 크기가 커질 경우 매우 비효율적이기 때문임.단, $3\times 3$ 이하의 작은 크기이거나, Complex Number 로 인해 Row Reduction 등이 효과적이지 못한 경우에는 inverse를 구하는데 사용되기도 함.주요 용도는 Theoretical Tool로서 inverse를 다 구하지 않고도, $A\mathbf{x}=\mathbf{b}$에서 $\mathbf{b}$의 작은 변화가$\mathbf{x}$에 얼마나 영향을 주는지 등을 살피는 것임. 주요행렬이 방식에서 중간..

Quadratic Form : Scalar 에서 이차식 (Quadratic Expression) $a x^2$의 일반형. Definition of Quadratic Form$x\in \mathbb{R}^n$ 일 때, $\mathbb{R}^n$에서의 Quadratic Form (이차형식) 은 다음과 같음. $$\mathbf{x}^\top A \mathbf{x}$$ where,$A$: Matrix of Quadratic Form. 이차항에서의 coefficient에 해당함.항상 Symmetric Matrix임.$n=1$인 경우, $a x^2$가 이차형식으로 scalar가 됨: $1 \times 1$.Hessian 의 부호: Concave, Convex$f(x)=a x^2$ 와 같은 이차식은 concave, co..

ML 을 위해 Linear Algebra 공부시 참고할만한 책더보기전체적으로 공부를 한다면 다음을 권함.Linear Algebra and Its Application, 5th ed 이상, David C. Lay5th ed. 는 웹에서 쉽게 pdf도 구할 수 있음.개인적으로 Strang 교수님 교재보다 쉽게 읽혀짐.Practical Linear Algebra for Data Science,:From Core Concepts to Applications Using Python, Mike X Cohen. O'Reilly다음은 1~2개 챕터로 간단히 정리하는 경우.머신러닝을 위한 수학: 핵심 알고리즘 3가지로 배우는 최적화, 이병준, 2022, 한빛아카데미(주)1장 행렬 데이터 과학을 위한 기초수학 with 파..

특정 행렬 $A$는 linear transform을 의미함: $A\mathbf{x}$는 vector $\mathbf{x}$를 linear transform하는 것에 해당. Square Matrix $A$의 eigenvector와 eigenvalue는 $A$를 standard matrix로 하는 linear transform의 고유한 특성을 나타내는 요소임.주의할 점은 eigenvalue와 eigenvector의 정의로 인해 $A$는 항상 Square Matrix임.$A$가 rectangle matrix인 경우엔 Singular Value, PCA 등이 대신 사용됨: $AA^\top, A^\top A$를 응용.Definition:$$\begin{aligned}A\mathbf{x} &= \lambda \ma..

Definition: Rank ◁ matrix 속성The rank of a matrix $A$, denoted by rank $A$,is the dimension of the column space of $A$.Matrix를 이루는 Column Vectors에서 Linearly Independent 인 것들의 수를 의미Row Space의 Dimension 의 경우를 강조하여 Row Rank라고 부르고,Column Space의 경우를 강조하여 Column Rank라고도 부르는 경우가 있으나,동일한 Matrix에 대해 이 둘은 같기 때문에 그냥 Rank라고 지칭하는게 일반적임. $m \times n$ Matrix $A$에서 다음이 성립. $$ \text{Column Rank}(A) \le n \\ \text..