728x90
728x90
Time Invariant System and Time Varying System
$$y(t-t_0) = T\left\{ x(t-t_0) \right\}$$
- 시스템 특성(parameters)이 시간에 따라 불변(invariant)
- 시간에 상관없이 같은 입력에 대해서는 같은 반응을 나타냄
- 시불변이 아닌 시스템을 시변(time varying) 시스템이라고 한다.
가장 많이 모델링 및 분석되는 기본적인 system은
linear time-invariant system (LTI System)이기 때문에
Time Invariant System에 대한 확실한 이해가 중요함.
커피자판기는 time invariant system인가?
Causal System and Non-causal System
Causal System의 정의는 다음과 같음.
- 시스템의 어느 시점에서의 출력이 그 시점의 과거나 현재의 입력에 의해 결정되는 시스템(출력의 관점에서 본 정의)
- 시스템의 어느 시점에서의 입력이 그 시점의 현재나 미래의 출력에만 영향을 주는 시스템(입력에서 본 정의)
Causal System의 특징은 다음과 같음.
- 원인이 있어야 결과가 있다
- 미래의 입력이 현재의 출력에는 영향을 주지 못함
- $t_0$ 에서의 출력이 $t\le t_0$ 에서의 입력에만 의존
Non-causal System 은 Causal System이 아닌 것을 가르킴.
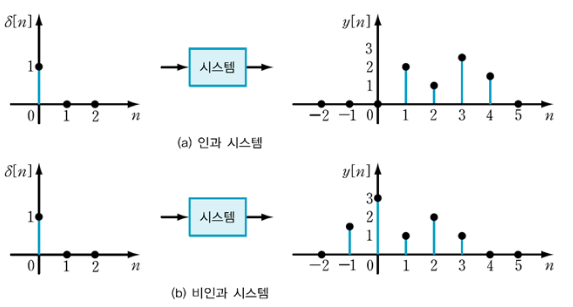
참고로, 수식적으로 봤을 때 공간과 관련된 imaging system등은 non-causal system과 같다. (독립변수들이 시간의 의미가 아닌 공간이 되는터라...)
728x90
'... > Signals and Systems' 카테고리의 다른 글
| [SS] Output of LTI System : Convolution with Impulse Response (0) | 2023.08.21 |
|---|---|
| [SS] System의 종류 (3) (0) | 2023.08.21 |
| [SS] System의 종류 (1) : Continuous, Linear (0) | 2023.08.21 |
| [SS] System 이란? (0) | 2023.08.21 |
| [SS] Properties of Impulse Function (0) | 2023.08.21 |