Example:
다음과 같은 미분 방정식을 2nd canonical form으로 표현.
$$\begin{aligned}(D^2+3D+2) y(t) &= D x(t)\end{aligned}$$
- $D$ : 미분연산자.
우선 적분기를 사용하기 위해 미분연산자를 제거.
$$D^{-2}[(D^2+3D+2) y(t)] = D^{-2}[D x(t)] \\ (1+3D^{-1}+2D^{-2}) y(t) = D^{-1} x(t)$$
중간변수 $v(t)$를 도입.
$$(1+3D^{-1}+2D^{-2}) y(t) = D^{-1} x(t) \\ y(t)=\frac{D^{-1}}{1+3D^{-1}+2D^{-2}} x(t) \\
y(t) = D^{-1} \frac{x(t)}{1+3D^{-1}+2D^{-2}} \\ y(t) = D^{-1} v(t)
$$
- $v(t)= \frac{x(t)}{1+3D^{-1}+2D^{-2}}$
이를 integrator, scalar multiplier, adder로 표현하면 다음과 같음.

$v(t)$를 $x(t)$로 표현 (1st canonical form과 유사)
$$ v(t)= \frac{x(t)}{1+3D^{-1}+2D^{-2}} \\ (1+3D^{-1}+2D^{-2})v(t) = x(t) \\
v(t)+ 3D^{-1}v(t) + 2D^{-2}v(t) = x(t) \\ v(t) = - 3D^{-1}v(t) - 2D^{-2}v(t) + x(t) $$
이를 integrator, scalar multiplier, adder로 표현하면 다음과 같음.

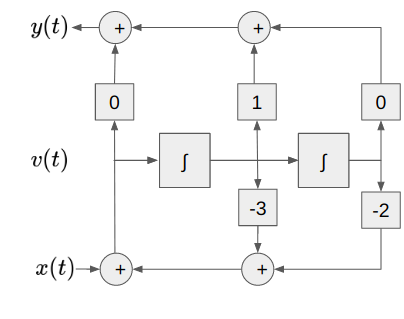
이를 결합하면 다음과 같은 2nd canonical form이 나옴.
관련 동영상
위의 미분방정식은 다음의 RLC circuit으로부터 유도된 것임.
2023.08.22 - [.../Signals and Systems] - [SS] RLC Circuit & Differential Eq
[SS] RLC Circuit & Differential Eq
다음의 RLC회로를 미분방정식으로 풀기 위의 회로에서 입출력 및 초기조건은 다음과 같음. input : $x(t) = 10e^{-3t}u(t)$ (voltage) output : $y(t)$ (current) initial condition : $y(0)=0$, $V_c(0)=5$ $u(t)$ : unit step function.
dsaint31.tistory.com
참고자료
1st canonical form에 대한 내용은 다음을 참고
2023.08.22 - [.../Signals and Systems] - [SS] Differential Equation : 1st Canonical Form
[SS] Differential Equation : 1st Canonical Form
Differential Equation은 3가지의 subsystem을 조합하여 구현할 수 있음.adder : 흔히 입력이 2개의 signal이고 출력은 두 입력 singal들을 더한 signal임.multiplier : scalar mulitplier로 승수가 scalar인 곱셈기. 입력 sing
dsaint31.tistory.com
2023.10.03 - [.../Signals and Systems] - [SS] 1st canonical form and 2nd canonical form
[SS] 1st canonical form and 2nd canonical form
1st canonical form(제1표준형)과 2nd canonical form(제2표준형)은 서로 transpose (전치관계)임 즉, 입력과 출력을 바꾸고 화살표의 방향을 반대로 하면 동일해짐. 위의 그림은 다음의 differential equation에 대한
dsaint31.tistory.com
'... > Signals and Systems' 카테고리의 다른 글
| [SS] Differential Equation : 1st Canonical Form (0) | 2023.08.22 |
|---|---|
| [SS] RLC Circuit & Differential Eq (0) | 2023.08.22 |
| [SS] Causal LTI System and Convolution (0) | 2023.08.22 |
| [SS] Convolution Example : Pulse Function (0) | 2023.08.22 |
| [SS] Convolution Op.에서 교환법칙 증명. (0) | 2023.08.21 |