...

[Math] Bernoulli Distribution (베르누이 분포)

Bernoulli distribution (베르누이 분포)은 Probability Distribution에서 가장 단순한 분포 중 하나 임. 주로 binary classification task에서 많이 사용됨. Bernoulli Trial 결과가 2가지 중 하나로만 나오는 trial(시행, 시도, 실험)을 가르킴. 대표적인 예로 동전 던지기(Head or Tail)가 Bernoulli trial에 해당. Bernoulli Random Variable Bernoulli trial의 결과를 숫자 0,1 (또는 -1, 1)로 할당한 random variable(확률변수). discrete random variable 로 2개의 값 중 하나만 가질 수 있는 특징을 가짐. Bernoulli Distributio..

[DL] Softsign : tanh의 유사품

hyperbolic tangent (=tanh)와 유사한 함수. tanh 대신 activation function으로 사용되는 경우도 있음. $$\text{softsign}(x)=\frac{x}{1+|x|}$$ softsign의 derivative는 다음과 같음. $$\dfrac{d}{dx}\text{softsign}(x)=\dfrac{1}{\left(1+|x|\right)^2}$$ 차트 비교 관련소스 import numpy as np import matplotlib.pyplot as plt x = np.linspace(-20.,20., 100) softsign = x/ (1.+np.abs(x)) logistic = 1/ (1+np.exp(-x)) tanh = np.tanh(x) fig,ax = plt...

[Math] Random Variable의 연산에 따른 Mean과 Variance.

Mean (or Estimated Value) Random Variable의 mean (여기선 arithmetic mean을 의미)은 linear equation으로 얻어짐. 때문에 다음과 같이 Random variable $X$와 $Y$, constant $a$와 $b$에 대해 linearity가 성립함. $E[a] =a$ $E[aX]=aE[X]$ $E[aX+b]=aE[X]+b$ $E[X+Y]=E[X]+E[Y]$ $E[aX+bY]=aE[X]+bE[Y]$ Random vairable간의 곱에서의 mean은 다음과 같이 구해짐. $E[XY]=\sum \sum xy P(X=x, Y=y)$ 결합확률분포에 대한 연산으로 두 random variable간의 correlation등의 고려등으로 계산이 복잡함. 만약..

[Math] log의 base 변환하기.

$$ \log_a b=x,\log_c a = y $$ 라고 할 경우 다음이 성립 $$ a^x=b, c^y=a \Rightarrow b=a^x=c^{yx} $$ log의 정의를 이용하면 다음이 유도됨. $$ b=c^{yx} \Rightarrow xy=\log_cb $$ $x=\log_a b, y=\log_c a$ 를 위 식의 left side에 대입하면 다음이 성립 $$ \log_a b \log_c a=\log_c b\\log_a b=\frac{\log_c b}{\log_c a} $$ 부가적으로 $c=b$인 경우엔 $$ \log_a b=\frac{\log_b b}{\log_b a}=\frac{1}{\log_b a} $$

[Math] log (logarithmic) function

Definition of Logarithmic Function $a>0, a\ne1$일 때 $x>0$인 $x$에 대하여 $a^y=x$이면 $$ y=\log_a x $$ 로 나타내고 $y$는 $a$를 base로 하는 logarithmic function 이라 한다. 이때, $x$를 $\log_a x$의 진수 (antilogarithm)라함. Exponential functions 의 inverse function 이 바로 logarithmic function임. $$x=a^y \rightarrow y=\log_a x$$ 이는 다음과 같이 애기할 수 있음. $$a^y=a^{\log_a x}=x$$ Common Log (상용로그) 고등학교까지는 common log를 $\log$로 표시하는 게 일반적이나, 대학..

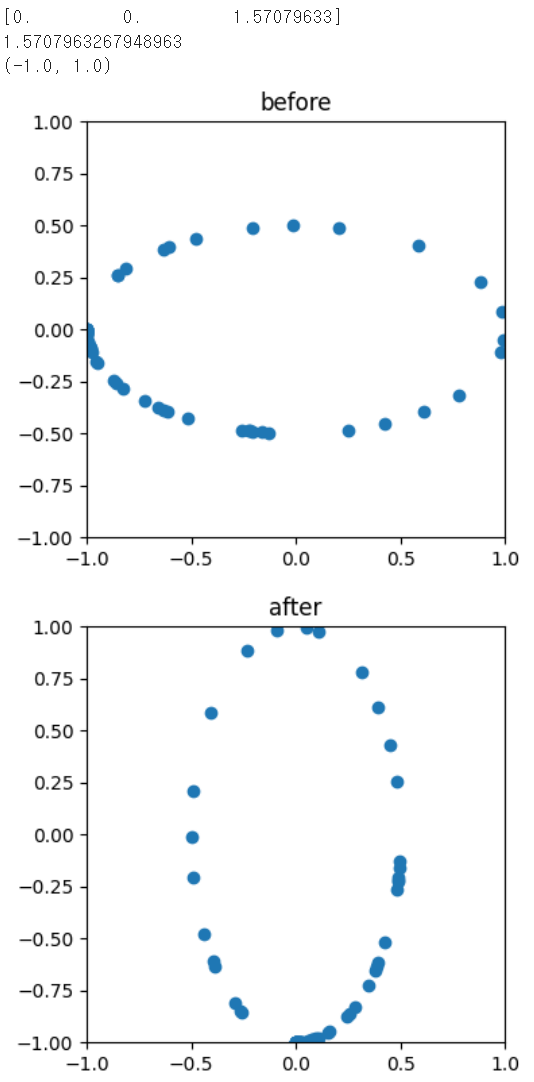
[Math] Rotation Vector (= Axis-Angle, Rodrigues Angle)

3차원 공간에서의 rotation을 표현하는 방법.Euler angle과 함께 가장 많이 사용되는 방법 중 하나임.하지만 3개의 축에 대한 3개의 rotation angle로 표현하는 Euler angle과 달리,Rotation Vector는 하나의 vector만으로 표현한다.컴퓨터 비전과 3D 그래픽스에서 자주 사용되며, 카메라 캘리브레이션, 객체 추적, 포즈 추정 등에 중요함.정의3차원 공간에서의 rotation은 회전축과 회전각이 필요한데Rotation Vector는회전축 : Rotation Vector의 direction으로 표현, $\mathbf{e}$.회전각 : Rotation Vector의 length로 표현 (L-2 norm), $\theta$일반적으로 회전중심은 origin이 됨.Axis..

[ML] Cosine Similarity

ML에서 주로 다루는 데이터는 바로 vector이다. (matrix도 vector들이 결합하여 이루어진 것이라고 생각할 수 있음.) Cosine Similarity는 두 vector가 얼마나 유사한지(similar)를 측정하기 위한 metric 중 하나로서, vector가 가지는 magnitude와 direction 두가지 특성 중에서 direction을 이용한다. 두 vector의 사이각 을 이용하여 similarity를 측정. 공식 공식은 다음과 같음. $$\text{cosine_similarity}=\cos \theta = \frac{\textbf{x}\cdot\textbf{y}}{\|\textbf{x}\|_2\|\textbf{y}\|_2}$$ \(\cdot\) : inner product (내적,..

[Math] Sequence (수열) and Series (급수)

Sequence 수열, 열 이라고 불림. numbers나 objects 들이 순서를 가지고(ordered) 나열된 것을 가르킴. order(순서)가 의미를 가지며, (order가 다르기 때문에 )중복이 허용이 된다. 중복이 허용된다는 점과 순서가 의미를 가진다는 점이 set과 가장 큰 차이점들임. sequence에서는 1,2,3과 2,1,3, 3,1,2 모두 다른 sequence임(구성하고있는 number는 같지만 순서가 다름.) 이들을 set이라고 본다면 같은 set이 됨. Python의 list, str, tuple등이 sequence를 추상화한 class이다. 순서가 의미를 가지므로 index로 사용됨. Series 급수라고 불리며, Sequence의 모든 항들을 더한 것을 가르킴. Sequece와..

[Math] Stationary point (or Critical point)

Stationary point (or Critical point, 정류점)(Convex) Opimization에서 찾고자하는 solution은 objective function에 대한 local minimum이다.이를 곧바로 찾기는 쉽지 않기 때문에, solution이 될 수 있는 후보들을 먼저 gradient (or 1st derivative)를 이용하여 찾아낸다.Convex optimization에서 solution에서 objective function의 gradient $\nabla f$는 반드시 $\textbf{0}$여야 한다 (역은 항상 true라고 보장 못함. 즉 necessary condition).정의$\nabla f(\textbf{x}^*)=0$ 를 만족하는 $\textbf{x}^*$를 ..

[Math] Second Order Condition : Convexity

First order condition과 함께 convexity를 판정하는 조건. Real vector space $\mathbb{R}^n$에서 $f:\mathbb{R}^n \to \mathbb{R}$이 second derivative 를 구할 수 있다면, 다음의 두 조건이 필요충분조건임. $f$ 는 convex function임. $\text{dom }f$는 convex set이고, 이에 속하는 임의의 $\textbf{x} \in \text{dom }f$에 대해 $\nabla^2 f(\textbf{x})$는 positive semi-definite 임. ($\nabla^2 f(\textbf{x})$ 은 vector에 대한 vector의 미분이라 matrix임.) $f$가 이차미분 가능하고 연속 함수인 ..