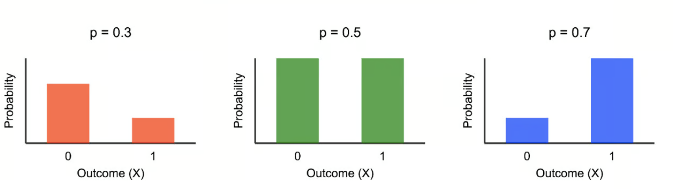
Bernoulli distribution (베르누이 분포)은 Probability Distribution에서 가장 단순한 분포 중 하나 임.
주로 binary classification task에서 많이 사용됨.original: https://www.datacamp.com/tutorial/bernoulli-distribution
1. Bernoulli Trial
결과가 2가지 중 하나로만 나오는 trial(시행, 시도, 실험)을 가르킴.
- 대표적인 예로 동전 던지기(Head or Tail)가 Bernoulli trial에 해당.
2. Bernoulli Random Variable
Bernoulli trial의 결과를 숫자 0,1 (또는 -1, 1)로 할당한 random variable(확률변수).
discrete random variable 로 2개의 값 중 하나만 가질 수 있는 특징을 가짐.
3. Bernoulli Distribution (Bernoulli Probability Distribution)
Bernoulli random variable의 distribution(분포)임.
random variable $X$가 Bernoulli distribution에 따라 값을 가진다면 다음과 같이 표기.
$$ X \sim \text{Bern}(x;\mu) $$
- $\mu$는 확률변수 $X$가 1이 될 확률임. [0.0, 1.0]
3-1. Probability Mass Function
Probability Mass Function (pmf)은 다음과 같음.
$$ \begin{aligned}\text{Bern}(x;\mu)&=\left\{\begin{matrix}\mu & \text{if }x=1,\\1-\mu& \text{if }x=0\end{matrix}\right.\\&=\mu^x (1-\mu)^{1-x}\end{aligned} $$
Bernoulli distribution에서 parameter는 $\mu$ 로서 1이 나올 확률임.
만약 결과값이 0,1이 아닌 -1, 1인 경우, probability mass function (pmf) 은 다음과 같음.
$$ \text{Bern}(x;\mu)=\mu^{(1+x)/2}(1-\mu)^{(1-x)/2} $$
3-2. Binomial Probability Distribution과의 관계
참고로 Bernoulli trial을 여러번 수행할 때의 성공횟수는
Binomial distribution을 따름.
2023.03.14 - [.../Math] - [Math] Binomial Distribution (이항분포)
[Math] Binomial Distribution (이항분포)
Binomial Distribution (이항분포) :1. 정의 1이 나올 확률(or 성공확률)이 $p$이고, 0이 나올 확률(or 실패확률)이 $1-p$인 Bernoulli trial을 $N$번 반복하는 경우의 성공횟수를 Random Variable $X$라고 할 경우, $X$가
dsaint31.tistory.com
4. Moment
4-1. expected value (기댓값)
$$ E[X]=\mu $$
proof:
$$ \begin{aligned}E[X]&=\sum_{x_i\in\Omega}x_ip(x_i)\\&=1\mu+0(1-\mu)\\&=\mu\end{aligned} $$
4-2. variance (분산)
$$ \text{Var}[X]=\mu(1-\mu) $$
proof:
$$ \begin{aligned}\text{Var}[X]&=\sum_{x_i\in\Omega}(x_i-\mu)^2p(x_i)\\&=(1-\mu)^2\mu+(0-\mu)^2(1-\mu)\\&=\mu(1-\mu)\end{aligned} $$
같이보면 좋은 자료들
2024.04.18 - [.../Math] - [Math] Probability Distribution
[Math] Probability Distribution
Probability DistributionProbability Distribution은 특정 random variable(확률 변수)이 취할 수 있는 각각의 값에 대한 확률을 나타내는 분포임.Probability Distribution Function (PDF)으로 기술되며,random variable이 어떤 값
dsaint31.tistory.com
2025.05.08 - [.../Math] - [Summary] 확률 및 통계 기본
[Summary] 확률 및 통계 기본
기본 term 과 정의들.2024.02.23 - [.../Math] - [Math] 기본 Term: Statistics [Math] 기본 Term: Statistics기본 Term: Statistics기술 통계와 추론 통계의 주요 개념들, 그리고 관련 용어들에 대한 소개1. Statistics (통계)의
dsaint31.tistory.com
'... > Math' 카테고리의 다른 글
| [Math] Error Function (0) | 2023.09.24 |
|---|---|
| [Math] The Cauchy-Schwarz Inequality (0) | 2023.08.22 |
| [DL] Softsign : tanh의 유사품 (0) | 2023.08.15 |
| [Math] Random Variable의 연산에 따른 Mean과 Variance. (0) | 2023.08.14 |
| [Math] log의 base 변환하기. (0) | 2023.08.13 |