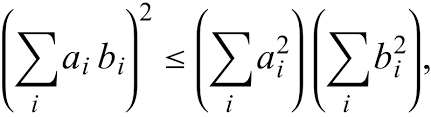
Triangular inequality와 함께 가장 많이 사용되는 inequality임.
2025.02.10 - [.../Math] - [Math] Triangular Inequality (삼각부등식)
[Math] Triangular Inequality (삼각부등식)
Definition$$\| \mathbf{u} + \mathbf{v} \| \le \|\mathbf{u}\| + \|\mathbf{v}\|$$증명https://youtu.be/4Q6kMzzVgcw 같이보면 좋은 자료들https://bme808.blogspot.com/2022/10/norm.html Norm (노름)Vector 및 matrix의 크기에 해당하는 양(magn
dsaint31.tistory.com
Cauchy-Schwarz Inequality
Vector space $V$의 모든 vector $\textbf{u}$, $\textbf{v}$에 대해 성립하는 다음의 부등식 관계를 의미함.
$$|\langle\textbf{v},\textbf{u}\rangle | \le \|\textbf{v} \| \|\textbf{u}\|$$
where
- $\langle \textbf{u}, \textbf{v} \rangle$ : vector $\textbf{u}$와 $\textbf{v}$의 inner product.
- $|x|$ : scalar $x$에 대한 absolute value.
- $\|\textbf{u}\|$: $\textbf{u}$의 norm (주로 L2-norm을 사용).
증명.
$\textbf{u} = \textbf{0}$ 인 경우, Cauchy-Schwarz Inequality의 양 side가 0이되어 등식이 성립.
$\textbf{u} \ne \textbf{0}$ 인 경우, $\textbf{u}$에 의한 spanned subspace $W$에 대해 $\textbf{v}$를 projection으로부터 Cauchy-Schwarz Inequaility가 유도됨.
$$ \begin{aligned}\|\text{proj}_W\textbf{v}\|&=\left \|\frac{\langle\textbf{v},\textbf{u}\rangle}{\langle \textbf{u},\textbf{u} \rangle}\textbf{u} \right\| \quad \leftarrow \|c\textbf{u}\|=|c|\|\textbf{v}\|\\ &= \left| \frac{\langle \textbf{v}, \textbf{u} \rangle}{\langle \textbf{u}, \textbf{u} \rangle} \right| \|\textbf{u}\| \\ &= \frac{|\langle\textbf{v},\textbf{u}\rangle|}{|\langle \textbf{u},\textbf{u} \rangle|}\|\textbf{u}\| \\ &= \frac{|\langle\textbf{v},\textbf{u}\rangle|}{\|\textbf{u} \|^2}\|\textbf{u}\| \\ &= \frac{|\langle\textbf{v},\textbf{u}\rangle|}{\|\textbf{u} \|} \end{aligned}$$
$\| \text{proj}_W \textbf{v}\| \le \|\textbf{v}\|$가 항상 성립하므로 다음을 얻을 수 있음.
$$\frac{ | \langle \textbf{v}, \textbf{u} \rangle | }{\| \textbf{u} \|} \le \|\textbf{v}\| \\ | \langle \textbf{v}, \textbf{u} \rangle | \le \|\textbf{v} \| \|\textbf{u}\| $$
참고자료
https://blog.naver.com/skkong89/222469897198
코시-슈바르츠 부등식 Cauchy-Schwarz's Inequality 간단 설명 (STAT-110)
본 내용은 STAT-110 강의 28번의 일부 내용 정리입니다. 자세한 내용은 해당 강의를 참고하세요. 이 교...
blog.naver.com
코시-슈바르츠 부등식의 증명 (동영상) | 벡터의 내적과 외적 | Khan Academy
수학, 예술, 컴퓨터 프로그래밍, 경제, 물리학, 화학, 생물학, 의학, 금융, 역사 등을 무료로 학습해 보세요. 칸아카데미는 어디에서나 누구에게나 세계 최고의 무료 교육을 제공하는 미션을 가진
ko.khanacademy.org
https://bme808.blogspot.com/2022/10/norm.html
Norm (노름)
Vector 및 matrix의 크기에 해당하는 양(magnitude) 을 구하는 연산 으로 사용됨. The higher the norm index($p$값이 클 경우), the more it focuses on large values ...
bme808.blogspot.com
'... > Math' 카테고리의 다른 글
| [Math] Derivative of Logistic Function (0) | 2023.09.25 |
|---|---|
| [Math] Error Function (0) | 2023.09.24 |
| [Math] Bernoulli Distribution (베르누이 분포) (0) | 2023.08.17 |
| [DL] Softsign : tanh의 유사품 (0) | 2023.08.15 |
| [Math] Random Variable의 연산에 따른 Mean과 Variance. (0) | 2023.08.14 |