Probability Distribution :
Probability Distribution은 특정 random variable(확률 변수)이 취할 수 있는 각각의 값에 대한 확률을 나타내는 분포임.
- Probability Distribution Function (PDF)으로 기술되며,
- random variable이 어떤 값을 얼마나 자주 취하는지를 나타냄.
- 이를 통해 random variable의 특성과 동작을 이해할 수 있음.
일반적으로 PDF는 probability density function의 약어이나,
이 문서에서는 probability distribution function의 약어로 사용함.
즉, 이 문서에서의 PDF는 cumulative distribution function과 같은 뜻임을 주의할 것.
Definition of PDF
random variable $X$가 가질 수 있는 특정한 value $x$와 이 $x$에 대응하는 확률을 매핑하고 있는 function.
- PDF는 abbreviation of Probability Distribution Function.
- pdf는 probability density function.
$$
P_X(C)=Pr[X\le C]
$$
- $Pr[X \le C]$ : 확률변수 $X$가 $C$보다 같거나 작은 값을 가질 확률.
이 PDF는 다음의 성질을 가짐.
- $0\le P_X(C)\le 1$
- $P_X(-\infty)=0$
- $P_X(\infty)=1$
- $P_X(C_1) \le P_X(C_2)$, for $C_1 \le C_2$
다른 이름으로는
cumulative distribution function (cdf)라고도 불림.
다음과 같이 뒤에 다루는 pmf 또는 pdf의 적분 형태로 기재할 수 있음.
- $\text{cdf}(c)=\displaystyle \sum_{x\le c} \text{pmf}(x)$
- $\text{cdf}(c)=\displaystyle \int_{-\infty}^c \text{pdf}(x) dx$
Exampe of PDF
두 개의 동전을 던졌을 때, 앞면이 나오는 횟수를 random variable X라고 할 경우, probability distribution은 다음과 같음.
| $X$ | $p(X=x)$ | $PDF(X=x)$ |
| 0 | 1/4 | 1/4 |
| 1 | 1/2 | 3/4 |
| 2 | 1/4 | 4/4=1 |
pdf and pmf
probability mass function (확률질량함수, pmf)
- discrete random variable (취할 수 있는 값이 유한하거나 셀수 있음) 의 probability distribution (확률분포)를 기재.
- $f(x)=\left\{\begin{matrix}p(X=x_i) & x=x_i (i=1,2,\dots,k) \\ 0 & \text{others} \end{matrix}\right.$
- 모든 $X$에 대해 $f(x)\ge0$
- $\displaystyle \sum_S f(x)=1$
- $S$ : sample space : $x\in S$
probability density function (확률밀도함수, pdf)
- continuous random variable (취할 수 있는 값이 연속적으로 셀 수 없음=무한개) 의 probability distribution (확률분포)를 기재.
- 확률변수 $X$와 확률밀도의 관계를 나타내는 함수.
- 특정값에 대한 pdf의 값은 0임. (구간으로 입력해야 값을 가짐) : $\int_c^cf(x)dx=0$
- 특정 구간에 대한 적분값은 0이상.
- 확률변수 $X$가 두 수 $x_1$와 $x_2$ 사이에 놓일 확률은 pdf $f(x)$의 아래 $x_1$과 $x_2$ 사이의 면적과 같다.
- $p(x_1 \le X \le x_2) = \displaystyle \int_{x_1}^{x_2} f(x)dx$
- 전체 면적은 1.
- $\underset{S}{\int} f(x) dx = 1$
- $S$ : sample space : $x\in S$
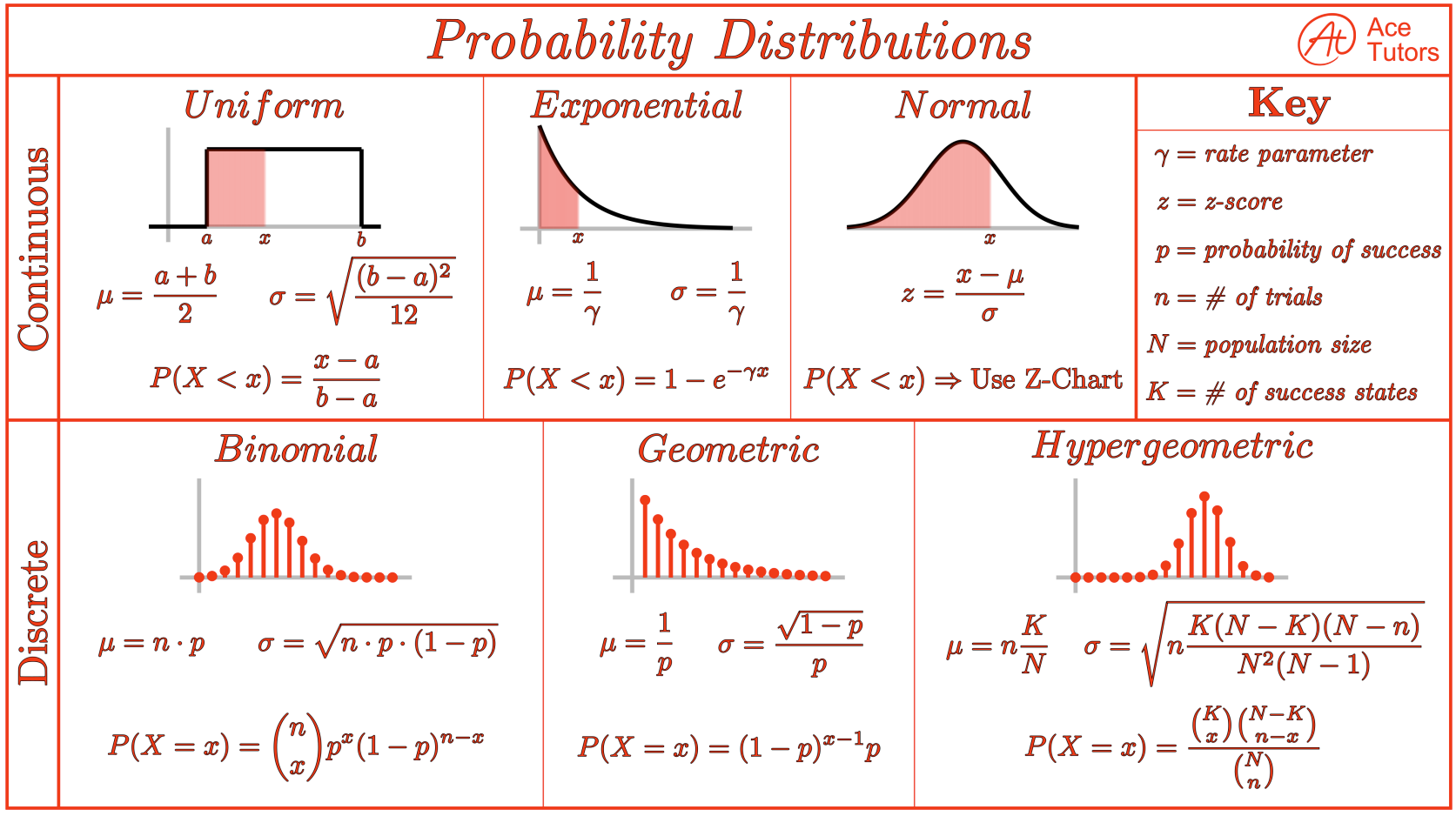
여러 Probability Distributions
각 확률분포들의 관계를 도식화하며 다음과 같음.

2023.10.25 - [.../Math] - [Math] Normal Distribution (정규분포)
[Math] Normal Distribution (정규분포)
Normal DistirbutionGaussian Distribution, Laplace-Gaussian Distribution 라고도 불림. 특히, mean=0이고, std=1인 경우, Standard Normal Distribution이라고 불림.1. 정의Normal Distribution의 PDF는 다음과 같음. $$f(X)=\frac{1}{\sigma\sq
dsaint31.tistory.com
2023.08.17 - [.../Math] - [Math] Bernoulli Distribution (베르누이 분포)
[Math] Bernoulli Distribution (베르누이 분포)
Bernoulli distribution (베르누이 분포)은 Probability Distribution에서 가장 단순한 분포 중 하나 임. 주로 binary classification task에서 많이 사용됨.1. Bernoulli Trial결과가 2가지 중 하나로만 나오는 trial(시행, 시
dsaint31.tistory.com
2023.03.14 - [.../Math] - [Math] Binomial Distribution (이항분포)
[Math] Binomial Distribution (이항분포)
Binomial Distribution (이항분포) :1. 정의 1이 나올 확률(or 성공확률)이 $p$이고, 0이 나올 확률(or 실패확률)이 $1-p$인 Bernoulli trial을 $N$번 반복하는 경우의 성공횟수를 Random Variable $X$라고 할 경우, $X$가
dsaint31.tistory.com
2024.05.22 - [.../Math] - [Math] Categorical Distribution
[Math] Categorical Distribution
Categorical Distribution일반적으로 multi-class classification (다중분류문제)에서 사용되는 확률분포.Categorical Random Variable$K$개(=class 갯수)의 정수값 중 하나를 가질 수 있는 확률변수.이때 가질 수 있는 $K$
dsaint31.tistory.com
2024.05.22 - [.../Math] - [Math] Multinomial Distribution (다항분포)
[Math] Multinomial Distribution (다항분포)
Multinomial Distribution : $K$ 개 class인 Categorical Variable의sample을 $N$개 얻을 때의각각의 class $i$가 각각 $x_i$번 나오는 random variable $\textbf{X}$의 이산 확률 분포. 달리 말하면 $\textbf{x}$가 $(x_1, x_2, \cdots, x_K
dsaint31.tistory.com
2023.10.25 - [.../Math] - [Math] Poisson Distribution (포아송분포)
[Math] Poisson Distribution (포아송분포)
Poisson Distribution이란?아주 가끔 일어나는 사건(trial)에 대한 확률 분포 : 방사선 검출에 주로 사용되는 확률분포라 의료영상에서는 매우 많이 사용됨.전체 인구수에서 연간 백혈병으로 사망 건수
dsaint31.tistory.com
2025.04.29 - [.../Math] - [Math] Gamma Distribution (링크 보완 필요)
[Math] Gamma Distribution (링크 보완 필요)
Gamma distribution은Poisson trial$(\sim \text{Poisson}(x;\lambda=\beta))$이$\alpha$회 발생할 때까지의 대기 시간이나타내는 (연속)확률분포임.참고로, exponential distribution은 최초($\alpha=1$)의 Poisson trial이 발생할 시
dsaint31.tistory.com
2025.04.29 - [.../Math] - [Math] Exponential Distribution
[Math] Exponential Distribution
Exponential Distrubtion지수 분포(Exponential distribution)의 수식은 다음과 같음:확률 밀도 함수(PDF):$$f(x; \lambda) =\begin{cases}\lambda e^{-\lambda x}, & x \geq 0 \\0, & x \end{cases}$$여기서:$x$는 랜덤 변수(관측값)$\lambda$
dsaint31.tistory.com
2025.01.13 - [.../Math] - [Math] Laplace Distribution
[Math] Laplace Distribution
Laplace 분포(Laplace Distribution) 소개Laplace 분포(Laplace Distribution)는 다음과 같은 특징을 가지는 연속확률분포임.sharp한 peak(정점)(Normal Distribution에 비해 더) 두꺼운 꼬리(heavy tails)를 가짐.double exponentia
dsaint31.tistory.com
같이 보면 좋은 자료들
2024.05.02 - [분류 전체보기] - [Math] Example: pmf, pdf, and cdf
[Math] Example: pmf, pdf, and cdf
27) Probability Mass Function (pmf)은 어떤 종류의 데이터에 사용됩니까? A) 연속 데이터 B) 이산 데이터 C) 양의 데이터 D) 음의 데이터 Ans. B) pmf는 discrete random variable에 대해 정의됨.28) Probability Density Funct
dsaint31.tistory.com
2023.03.09 - [.../Math] - [Math] Random Variable
[Math] Random Variable
Random Variable Random variable(확률변수)란 sample space의 event (=subset of sample space)들을 어떤 real number(실수)나 integer(정수) 등의 숫자들에 mapping한 것을 가르킨다. "Random process 나 Random trial (or Random experiment)
dsaint31.tistory.com
2024.04.17 - [.../Math] - [Math] Probability 란
[Math] Probability 란: Probability, Odds, Likelihood
Probability란 ? 어떠한 event(사건, 사상)의 공간(=sample space, 발생가능한 모든 sample points로 구성된 set)에서특정 event(or sample point의 set으로 sample space의 subset)가 선택될(발생할) 수 있는불확실성(uncertain
dsaint31.tistory.com
2024.02.23 - [.../Math] - [Math] Random이란?
[Math] Random이란?
RandomRandom은 주로 non-determinstic인 "정해진 패턴 또는 순서없이" 결과가 발생하는 것을 의미하는 경우가 많다. Deterministc인 경우,function (or differential equation) 등을 이용한 모델링을 통해,inputs 에 대한
dsaint31.tistory.com
'... > Math' 카테고리의 다른 글
| [Math] Example: Variable (0) | 2024.05.02 |
|---|---|
| [Math] The Law of Total Probability (0) | 2024.04.23 |
| [Math] 확률에서 Partition: Mutually Exclusive and Exhaustive (0) | 2024.04.18 |
| [Math] 확률의 법칙들 (0) | 2024.04.18 |
| [Math] Conditional Probability and Joint Probability (0) | 2024.04.17 |