Categorical Distribution
일반적으로 multi-class classification (다중분류문제)에서 사용되는 확률분포.
1. Categorical Random Variable
$K$개(=class 갯수)의 정수값 중 하나를 가질 수 있는 확률변수.
- 이때 가질 수 있는 $K$개의 정수값은 각각 class (또는 category) 에 해당함.
- 예를 들어, $K=2$인 경우, Bernoulli Random Variable과 동일.
- one-hot encoding을 사용하여 sample instance의 value가 vector로 나옴: moment들도 모두 vector임.
대표적으로 주사위 던지기를 들 수 있고, 이때 $K=6$ 임.
2. 주사위 예
$$\begin{aligned} x &= 1 \quad \rightarrow \quad \mathbf{x} = (1, 0, 0, 0, 0, 0) \\ x &= 2 \quad \rightarrow \quad \mathbf{x} = (0, 1, 0, 0, 0, 0) \\ x &= 3 \quad \rightarrow \quad \mathbf{x} = (0, 0, 1, 0, 0, 0) \\ x &= 4 \quad \rightarrow \quad \mathbf{x} = (0, 0, 0, 1, 0, 0) \\ x &= 5 \quad \rightarrow \quad \mathbf{x} = (0, 0, 0, 0, 1, 0) \\ x &= 6 \quad \rightarrow \quad \mathbf{x} = (0, 0, 0, 0, 0, 1) \end{aligned}$$
- 화살표 오른쪽에 있는 vector표현이 바로 one-hot encoding 임.
- $\textbf{x}=(x_1,x_2,x_3,x_4,x_5,x_6)$으로 일반형으로 표현됨.
- $x_i$는 0 or 1 만을 가질 수 있음.
- $\displaystyle \sum^K_{i=1}x_i = 1$이 성립.
즉, $K$ class인 경우, $\textbf{x}$는 $K$개의 element를 가지며, 오직 한 element만 1이고(=mutually exclusive), 나머진 0을 가짐. - $x_i$는 일종의 Bernoulli random variable이라고 볼 수 있으며, 각각의 $x_i$는 Bernoulli distribution을 따르므로 1이 될 확률 $\mu_i$를 가짐.
- $x_i$들을 한꺼번에 vector $\textbf{x}$로 표현하는 것처럼, $\mu_i$들을 모아 vector $\mu$로 표현함 (vector 표현이 보다 일반적임.
- $\mu=(\mu_1, \mu_2, \mu_3, \cdots, \mu_K)$
- vector $\mu$는 Categorical distribution의 parameter임.
- vector $\mu$는 다음의 조건을 만족함.
- $\mu_i$는 0 이상, 1이하의 값을 가짐 ($x_i$와 달리 연속변수임).
- $\displaystyle \sum^K_{i=1} \mu_i = 1$이 성립. $\mu_i$는 $i$ 번째 class에 속할 확률을 의미.
3. Categorical Distribution
Bernoulli distirbution에서
random variable이 0과 1만을 가지는 것을 1~ $K$ 의 integer값을 가지도록 확장(generalization)한 것.
즉, 파라메터(각 클래스가 될 확률)가 vector가 됨: $\mathbf{\mu}=(\mu_1, \dots, \mu_K)$
수식으로 다음과 같이 표현됨.
$$
\begin{aligned}\textbf{X}& \sim \text{Cat}(\textbf{x};\mu)\\ &\sim \text{Cat}(x_1,x_2,\cdots,x_K;\mu_1,\mu_2,\cdots,\mu_K)\end{aligned}
$$
- $x_i$: 카테고리 $i$에 대한 Bernoulli random variable. : 0 or 1을 가질 수 있음.
시행횟수를 여러 차례로 증가시킬 경우, Multinomial Distirbution이 됨.
2024.05.22 - [.../Math] - [Math] Multinomial Distribution (다항분포)
[Math] Multinomial Distribution (다항분포)
Multinomial Distribution : $K$ 개 class인 Categorical Variable의sample을 $N$개 얻을 때의각각의 class $i$가 각각 $x_i$번 나오는 random variable $\textbf{X}$의 이산 확률 분포. 달리 말하면 $\textbf{x}$가 $(x_1, x_2, \cdots, x_K
dsaint31.tistory.com
3-1. Probability Mass Function (pmf)
Probability Mass Function은 다음과 같음.
$$ \text{Cat}(\textbf{x};\mu)=\left{ \begin{matrix} \mu_1 & \text{if } \textbf{x}=(1,0,\cdots,0)\\ \mu_2& \text{if }\textbf{x}=(0,1,\cdots,0) \\ \vdots & \vdots \\ \mu_K & \text{if }\textbf{x}=(0,0,\cdots,1) \end{matrix} \right. $$
one-hot encoding을 사용했기 때문에 다음과 같은 축약형이 가능함.
$$ \text{Cat}(\textbf{x};\mu)=\mu_1^{x_1}\mu_2^{x_2}\cdots\mu_K^{x_K}=\prod_{i=1}^{K}\mu_i^{x_i}$$
3-2. Moment
sample value가 vector이므로, moment도 vector임.
moment의 각 element는 다음과 같음 (참고: Bernoulli distribution)
3-2-1. expected value
$$
E[x_i]=\mu_i
$$
3-2-2. variance
$$
\text{Var}[\mu_i]=\mu_i(1-\mu_i)
$$
4. scipy.stats.multinomial
multinomial은
사실 Multinomial distribution(다항분포)를 위한 것이나,
시행횟수 $N$이 1인 경우 Categorical Distibution이 됨.
(Bernoulli distribution과 Binomial distribution의 관계와 같음)
import numpy as np
import scipy
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
mu = [0.1,0.2,0.2,0.2,0.2,0.1]
N = 1
rv = scipy.stats.multinomial(N, mu)
candidates = np.arange(1,7)
candidates_onehot = pd.get_dummies(candidates)
plt.bar(candidates, rv.pmf(candidates_onehot.values))
plt.ylabel('p(x)')
plt.xlabel('sample value')
plt.title('PMF of Categorical Distribution')
plt.show()결과

<확률분포클래스의 인스턴스>.rvs를 통한 sampling: rvs=Random Variates의 약자.
np.random.seed(973037)
x = rv.rvs(100)
print(x[:3])[[0 1 0 0 0 0] [0 0 0 0 1 0] [0 0 0 0 1 0]]
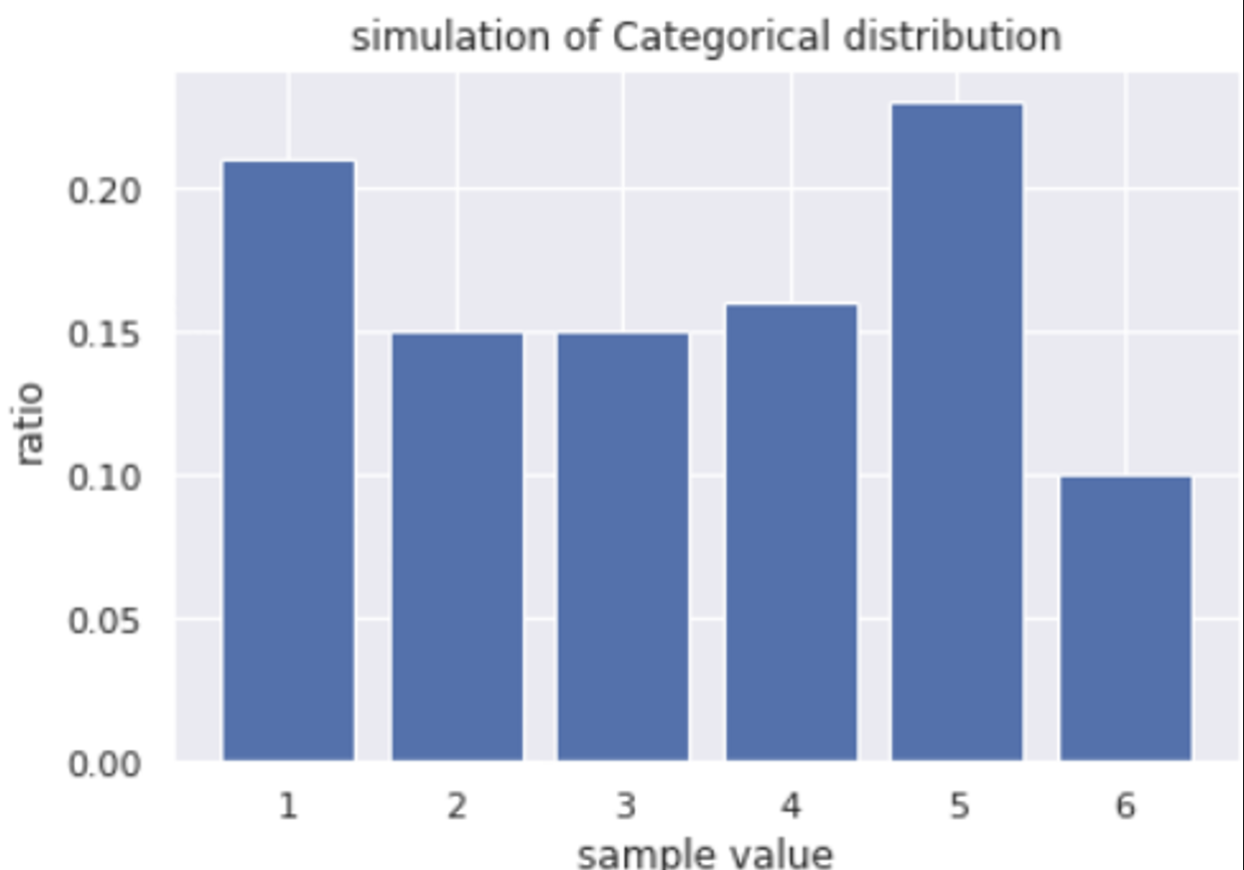
Simulation
measured = x.sum(axis=0) / float(len(x))
plt.bar(candidates, measured)
plt.title('simulation of Categorical distribution')
plt.xlabel('sample value')
plt.ylabel('ratio')
plt.show()결과
Ideal vs. Simulation
df = pd.DataFrame({'ideal': rv.pmf(candidates_onehot.values), 'measured':measured})
df.index = candidates
df2 = df.stack().reset_index()
df2.columns = ['sample value','type','ratio']
#df2.pivot('sample value','type','ratio')
sns.barplot(x='sample value', y='ratio', hue='type', data=df2)
plt.title('ideal vs. measured')
plt.show()결과

같이보면 좋은 자료들
2024.04.18 - [.../Math] - [Math] Probability Distribution
[Math] Probability Distribution
Probability DistributionProbability Distribution은 특정 random variable(확률 변수)이 취할 수 있는 각각의 값에 대한 확률을 나타내는 분포임.Probability Distribution Function (PDF)으로 기술되며,random variable이 어떤 값
dsaint31.tistory.com
2025.05.08 - [.../Math] - [Summary] 확률 및 통계 기본
[Summary] 확률 및 통계 기본
기본 term 과 정의들.2024.02.23 - [.../Math] - [Math] 기본 Term: Statistics [Math] 기본 Term: Statistics기본 Term: Statistics기술 통계와 추론 통계의 주요 개념들, 그리고 관련 용어들에 대한 소개1. Statistics (통계)의
dsaint31.tistory.com
'... > Math' 카테고리의 다른 글
| [Math] Optimization Problem 의 종류 (0) | 2024.06.01 |
|---|---|
| [Math] Optimization 이란 (Introduction) (0) | 2024.06.01 |
| [Math] Multinomial Distribution (다항분포) (0) | 2024.05.22 |
| [Math] Example: Variable (0) | 2024.05.02 |
| [Math] The Law of Total Probability (0) | 2024.04.23 |