[Math] Optimization Problem 의 종류

Optimization Problem의 종류

GD에 대한 그림으로 Goal의 형태가 일종의 Optimization이라고 보면 된다.

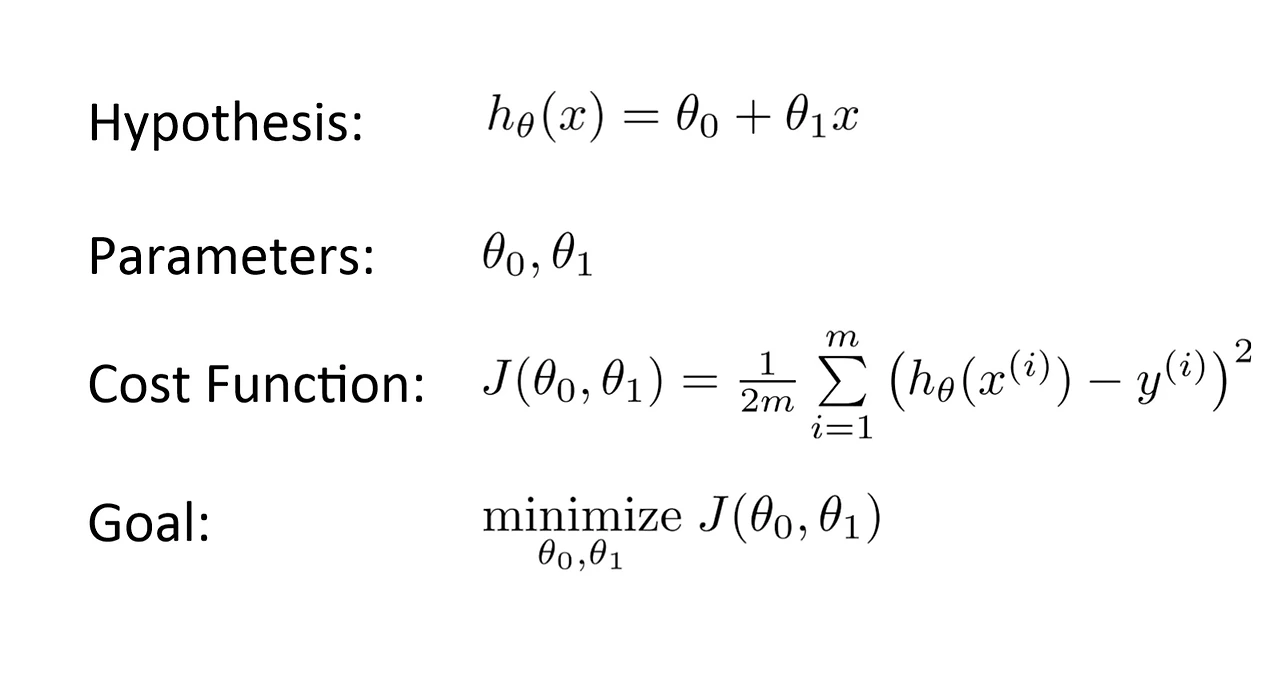
1. Minimization Problem vs. Maximization Problem

일반적인 최적화 문제 는 최소화 문제로 공식화될 수 있음.

 

이는 다음과 같이 표현됨:

$$
\underset{\boldsymbol{\omega}}{\min} f(\boldsymbol{\omega})
$$

이는 다음의 제약 조건에 종속됨:

• $m$개의 부등식 제약 조건: $g_i(\boldsymbol{\omega}) \le 0$
• $p$개의 등식 제약 조건: $h_j(\boldsymbol{\omega}) = 0$

여기서:

• $f(\boldsymbol{\omega})$: $\boldsymbol{\omega}$의 scalar-valued objective function (실값 함수 또는 스칼라 필드)
• $\boldsymbol{\omega}$: 입력 열 벡터 $\boldsymbol{\omega} = (\omega_0, \omega_1, \dots, \omega_n)^\top$ 또는 scalar 로 optimization variable 임.
• $\boldsymbol{g(\boldsymbol{\omega})}, \boldsymbol{h(\boldsymbol{\omega})}$: vector-valued constraint functions

이를 이를 optimization problem의 standard form 으로 기재하면 다음과 같음:

$$\begin{aligned} &\underset{\boldsymbol{\omega}}{\min} && f(\boldsymbol{\omega}) \\ &\text{subject to} && g_i(\boldsymbol{\omega}) \le 0,\quad i = 1,\dots,m \\ &&& h_j(\boldsymbol{\omega}) = 0,\quad j = 1,\dots,p \end{aligned}$$

 

함수의 매핑 관계는 다음과 같음:

$$
f: \mathbb{R}^n \rightarrow \mathbb{R} \\
\mathbf{g}: \mathbb{R}^n \rightarrow \mathbb{R}^m \\
\mathbf{h}: \mathbb{R}^n \rightarrow \mathbb{R}^p
$$

maximization(최대화) 문제의 경우,
해당 함수에 $-1$을 곱하면 equivalent 한
miniziation(최소화) 문제가 됨.
이는 miniziation 문제만 고려해도 충분함을 의미함.

 

최적화 문제는 objective function $f$와 constraint functions $\mathbf{g},\mathbf{h}$의 성질등에 따라 분류됨.

---

2. 입력에 의한 분류

2-1. Univariate Optimization Problem (단변수 최적화 문제)

$\boldsymbol{\omega}$는 scalar임 ($1\times 1$ matrix로 생각해도 됨).

즉,

• 입력 변수가 1개인 최적화 문제이며,
• convex optimization 등을 처음 배울 때 자주 등장하는 예제들이 여기에 해당함.

---

2-2. Multivariate or Multidimensional Optimization Problem (다변수 또는 다차원 최적화 문제)

$\boldsymbol{\omega}$는 vector임.

• 입력 변수가 여러 개인 최적화 문제이며,
• 일반적으로 objective function의 차원 $n$이 커질수록 문제를 푸는 것이 더 어려워지고 계산 비용도 증가함.

---

3. Linearity에 의한 분류

3-1. Linear Programming Problem (선형 계획 문제)

Objective function(목적 함수)과 constraints(제약 조건)가 모두 linear(선형) 일 경우를 가리킴.
(bias를 따로 표기하면 affine)

 

즉, objective function과 제약 조건이 모두 선형 구조를 가지는 최적화 문제임.

 

이 최적화 문제는 선형 최적화 문제 또는 linear programming(선형 계획) 문제로 불림.

2023.07.08 - [.../Math] - [Math] Linear Programming and Quadratic Programming

[Math] Linear Programming and Quadratic Programming

---

3-2. Nonlinear Programming Problem (비선형 계획 문제)

Objective function(목적 함수)이나 constraints(제약 조건) 중 하나라도 비선형인 경우,

이는 비선형 최적화 문제 또는 nonlinear programming problem(비선형 계획 문제)임.

즉, 선형 구조만으로는 표현되지 않는 최적화 문제를 의미함.

---

4. Constraints 유무에 의한 분류

Unconstrained Problem and Constrained Problem (비제약 문제와 제약 문제)

Constraints(제약 조건)에 따라 Optimization(최적화)의 중요한 하위 클래스는

• unconstrained problem(비제약 문제)와
• 선형 및 비선형 제약 조건을 가진 constrained problem(제약문제)들임.

또한 constrained problem에서는

• equality constraints(등식 제약 조건)
• inequality constraints(부등식 제약 조건)

을 어떻게 처리하느냐에 따라 사용하는 해법이 달라짐.

 

즉, 등식 제약 조건과 부등식 제약 조건은 수학적으로 역할이 다르므로, 이를 다루는 optimization method 역시 서로 달라질 수 있음.

---

5. min 과  argmin 의 차이

Optimization problem을 기술할 때는 보통 다음과 같이 $\min$을 사용하여
"어떤 objective function을 최소화할 것인가"를 나타냄.

$$
\underset{\boldsymbol{\omega}}{\min} ; f(\boldsymbol{\omega})
$$

이 표기는 최소화해야 할 문제 자체를 나타내며,
결과로 얻어지는 것은 함수값의 최소값임.

 

반면,

실제로 Machine Learning이나 Deep Learning에서 우리가 구하고 싶은 것은
Objective Function을 최소값으로 만드는 입력값임.

 

이를 가리켜 optimizer(최적해) 또는 minimizer를 구한다고 하며 

이경우에는 $\arg\min$을 사용함.

$$
\arg\min_{\boldsymbol{\omega}} f(\boldsymbol{\omega})
$$

이는 "함수 $f(\boldsymbol{\omega})$를 최소로 만드는 $\boldsymbol{\omega}$의 값"을 뜻함.

즉,

• $\underset{\boldsymbol{\omega}}{\min} f(\boldsymbol{\omega})$: 최소값 자체
• $\underset{\boldsymbol{\omega}}{\arg\min} f(\boldsymbol{\omega})$: 그 최소값을 만드는 $\boldsymbol{\omega}$

예를 들어, 최적화 문제의 해를 $\boldsymbol{\omega}^{*}$라고 하면 다음과 같이 쓸 수 있음.

$$
\boldsymbol{\omega}^{*} \in \arg\min_{\boldsymbol{\omega}} f(\boldsymbol{\omega})
$$

여기서 $\boldsymbol{\omega}^{*}$는 objective function을 최소화하는 optimizer임.

 

따라서 일반적인 optimization problem의 정의를 쓸 때는 $\min$을 사용하는 것이 자연스럽고,
그 문제의 solution 또는 minimizer를 나타낼 때는 $\arg\min$을 사용하는 것이 더 정확함.

---

같이 읽어보면 좋은 자료들

2023.07.06 - [.../Math] - [Math] Lagrangian from Standard Form using Indicator Function

[Math] Lagrangian from Standard Form using Indicator Function

 

https://www.amazon.com/Numerical-Python-Scientific-Applications-Matplotlib/dp/1484242459

Numerical Python: Scientific Computing and Data Science Applications with Numpy, SciPy and Matplotlib

https://dsaint31.me/mkdocs_site/ML/ch09/op_summary/

BME