#SS

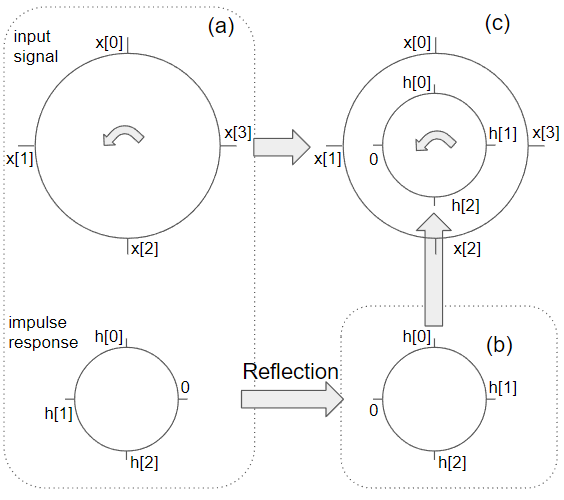
[SS] Circular Convolution

Circular Convolution이 필요한 이유. cyclic convolution이라고도 불림. DFT의 경우, frequency domain representation을 샘플링하므로, time domain representation도 periodic signal이 됨. 때문에 DFT에서 time domain에서 input signal x[n]과 impulse response h[n]을 convolution하여 zero-state response y[n]를 구하는 경우, 기존의 (linear) convolution이 아닌 circular convolution으로 구해야 DFT의 sampling으로 인해 time domain의 x[n]과 h[n]이 주기를 가지고 반복되게 된 점을 반영할 수 있음. c..

[SS] Properties of (unilateral) Laplace Transform

Unilateral Laplace Transform의 주요 성질. Linearity $$a{ x }_{ 1 }\left( t \right) +b{ x }_{ 2 }\left( t \right) \longleftrightarrow a{ X }_{ 1 }\left( s \right) +{ X }_{ 2 }\left( s \right)$$ Time Shifting $$x\left( t-{ t }_{ 0 } \right) u\left( t-{ t }_{ 0 } \right) \longleftrightarrow { e }^{ -s{ t }_{ 0 } }X\left( s \right)$$ $s$-domain Shifting (or Complex Shifting) $$x( t ) e^{ s_0 t} \longleft..

[SS] Laplace Transform : $\sin^2 \Omega_0 t u(t)$

$$\sin^2 t = \frac{1-\cos 2t}{2}$$ 를 이용한다. $\sin^2 \Omega_0 t$는 다음과 같이 전개가 가능함. $$\begin{aligned}\sin^2(\Omega_0 t)&=\frac{1-\cos 2\Omega_0t}{2}\\ &=\frac{1}{2}-\frac{1}{2}\cos 2\Omega_0t\end{aligned}$$ 이를 (Unilateral )Laplace transform하면 다음과 같음. $$\begin{aligned}\mathscr{L}\left[\sin^2\Omega_0 t\right]&=\mathscr{L}\left[\frac{1}{2}\right]-\mathscr{L}\left[\frac{1}{2}\cos 2\Omega_0t\right]\\ &=\..

[SS] Laplace Transform : $\cos^2 \Omega_0 t u(t)$

$$\cos^2 t = \frac{1+\cos 2t}{2}$$ 를 이용한다. $\cos^s \Omega_0 t$는 다음과 같이 전개가 가능함. $$\begin{aligned}\cos^2(\Omega_0 t)&=\frac{1+\cos 2\Omega_0t}{2}\\ &=\frac{1}{2}+\frac{1}{2}\cos 2\Omega_0t\end{aligned}$$ 이를 (Unilateral )Laplace transform하면 다음과 같음. $$\begin{aligned}\mathscr{L}\left[\cos^2\Omega_0 t\right]&=\mathscr{L}\left[\frac{1}{2}\right]+\mathscr{L}\left[\frac{1}{2}\cos 2\Omega_0t\right]\\ &=\..

[SS] Laplace Transform Table

Signal Laplace Transform RoC ... 1 $u(t)$ $\frac{1}{s}$ $\text{Re}(s)>0$ 2 $u(t)-u(t-a)$ $\frac{1-e^{-as}}{s}$ $\text{Re}(s)>0$ 3 $\delta(t)$ 1 all complex plane 4 $\delta(t-a)$ $e^{-as}$ all complex plane 5 $e^{-at}u(t)$ $\frac{1}{s+a}$ $\text{Re}(s)>-a$ 6 $\cos\Omega_0t u(t)$ $\frac{s}{s+\Omega_0^2}$ $\text{Re}(s)>0$ 7 $\sin\Omega_0t u(t)$ $\frac{\Omega_0}{s+\Omega_0^2}$ $\text{Re}(s)>0$ 8 $t^..

[SS] Ch04 Ex : Inverse Laplace Transform

1. 다음 $X(s)$의 Inverse Laplace Transform을 구하라. $$X(s)=\frac{8s^2-7s-6}{s^3-s^2-6s}$$ sol. $$\begin {aligned} X(s)&=\frac{8s^2-7s-6}{s^3-s^2-6s}\\ &=\frac{8s^2-7s-6}{s(s-3)(s+2)}\\ &=\frac{A}{s}+\frac{B}{s-3}+\frac{C}{s+2} \end {aligned}$$ distinct pole의 경우로서 다음과 같이 A,B,C를 구할 수 있음. $$ \begin {aligned} A&= \left. \frac{8s^2-7s-6}{(s-3)(s+2)} \right |_{s=0} \\ &= \frac{0-0-6}{-3\cdot 2} \\ &= 1 \end..