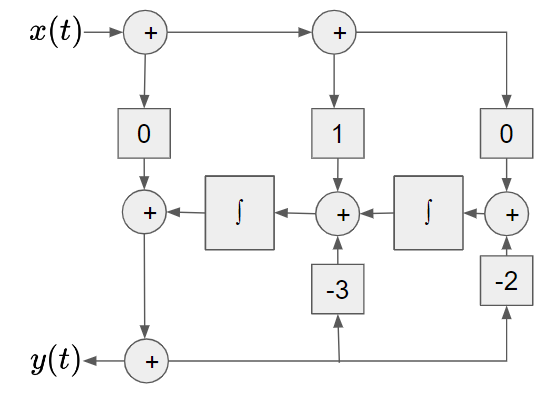
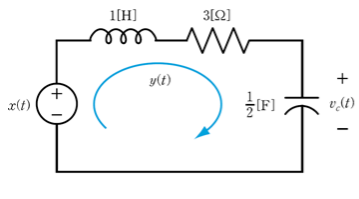
입력이 $x(t)$이고 최종출력이 $y(t)$인 parallel connection의 diagram은 다음과 같음. $h_1(t)$과 $h_2(t)$는 subsystem1과 subsystem2의 impulse response임. $y_1(t)$과 $y_2(t)$는 subsystem1과 subsystem2의 output임. 위와 같은 parallel connection system에서 impulse function이 입력되면 다음을 만족함. $x(t)=\delta(t)$ $y_1(t)=h_1(t)$ $y_2(t)=h_2(t)$ $y(t)=h(t)=h_1(t)+h_2(t)$ 즉, parallel connection의 경우 각 subsystem의 impulse response를 더함으로서 최종 impulse ..

입력이 $x(t)$이고 최종출력이 $y_2(t)$, 중간 출력이 $y_1(t)$인 cascade connection의 diagram은 다음과 같음. $h_1(t)$과 $h_2(t)$는 subsystem1과 subsystem2의 impulse response임. 입력이 impulse인 경우, 다음이 성립함. $x(t)=\delta(t)$ $y_1(t)=h_1(t)$ $y_2(t)=y_1(t)*h_2(t)=h_1(t)*h_2(t)$ 즉, subsystem1과 subsystem2의 cascade connetion을 큰 하나의 system으로 볼 수 있고, 이 경우 impulse response는 $h(t)=h_1(t)*h_2(t)$가 성립함. Subsystem들의 impulse response의 convolu..

문제다음 미분방정식 의 시스템이 있다고 하자$$ \frac{d^2 y(t)}{dt^2} + 3\frac{dy(t)}{dt}+2y(t)=\frac{dx(t)}{dt} $$ 아래와 같은 입력과 초기조건에서zero-state response (초기조건이 0.)zero-input response (input이 0.)natural response (system mode만으로 구성.)forced response (input signal에만 의한 항으로 구성.)를 구하라.input signal$$ x(t)=t^2+5t $$initial conditions$$ y(0^-)=2 \\ \frac{dy(0^-)}{dt} = 3 $$Sol 1. Classic MethodHomogeneous Solution 구하기Charact..

Laplace Transform을 이용한 Differential Equation을 풀기. 문제 다음 미분방정식 의 시스템이 있다고 하자. $$ \frac{d^2 y(t)}{dt^2} + 3\frac{dy(t)}{dt}+2y(t)=\frac{dx(t)}{dt} $$ 아래와 같은 입력과 초기조건에서 zero-state response (초기조건이 0.) zero-input response (input이 0.) natural response (system mode만으로 구성.) forced response (input signal에만 의한 항으로 구성.) 를 구하라. input signal $$ x(t)=t^2+5t $$ initial conditions $$ y(0^-)=2 \\ \frac{dy(0^-)}{..

Differential Equation은 3가지의 subsystem을 조합하여 구현할 수 있음. 1. adder : 흔히 입력이 2개의 signal이고 출력은 두 입력 singal들을 더한 signal임. 2. multiplier : scalar mulitplier로 승수가 scalar인 곱셈기. 입력 singal을 상수배하여 출력. 해당 상수배는 사전에 지정됨 3. integrator : 적분기로 적분이 수행되어 나옴. 입력이 $\dfrac{dx(t)}{dt}$ 인 경우, 출력이 $x(t)$로 적분되어 나옴. 위의 3가지 조합으로 differential equation을 기계적으로 표현하는 방법을 canonical form이라고 부르는데, 이 문서는 그중에서 1st canonical form (다른 이..

다음의 RLC회로를 미분방정식으로 풀기 위의 회로에서 입출력 및 초기조건은 다음과 같음. input : $x(t) = 10e^{-3t}u(t)$ (voltage) output : $y(t)$ (current) initial condition : $y(0)=0$, $V_c(0)=5$ $u(t)$ : unit step function. 1. Differential Equation KVL에 의하여 다음이 성립 $$\begin{aligned}{ V }_{ L }+{ V }_{ R }+{ V }_{ C }=x\left( t \right) \\ 1\frac { dy\left( t \right) }{ dt } +3y\left( t \right) +{ \frac { 1 }{ \frac { 1 }{ 2 } } }\int..