728x90
728x90
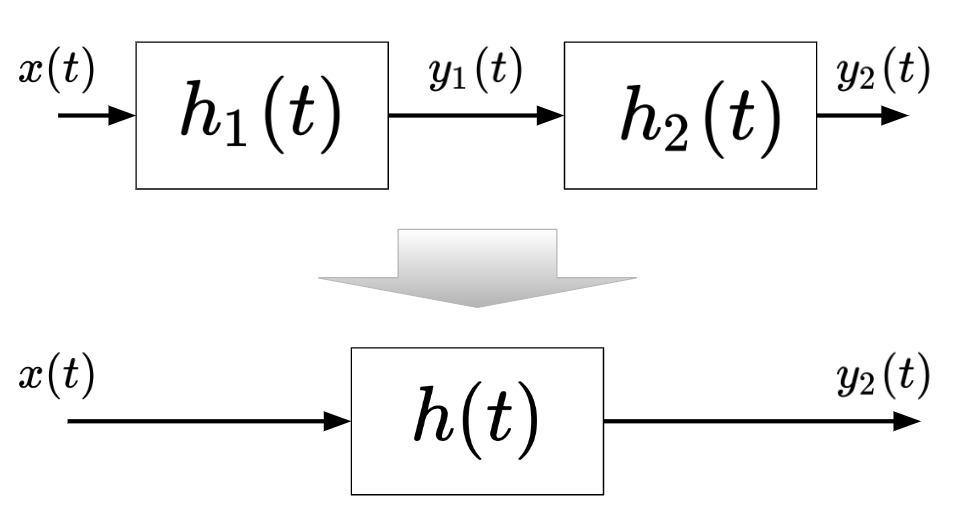
입력이 $x(t)$이고 최종출력이 $y_2(t)$, 중간 출력이 $y_1(t)$인 cascade connection의 diagram은 다음과 같음.
- $h_1(t)$과 $h_2(t)$는 subsystem1과 subsystem2의 impulse response임.
입력이 impulse인 경우, 다음이 성립함.
- $x(t)=\delta(t)$
- $y_1(t)=h_1(t)$
- $y_2(t)=y_1(t)*h_2(t)=h_1(t)*h_2(t)$
즉, subsystem1과 subsystem2의 cascade connetion을 큰 하나의 system으로 볼 수 있고, 이 경우 impulse response는 $h(t)=h_1(t)*h_2(t)$가 성립함.
Subsystem들의 impulse response의 convolution을 통해 전체 시스템의 impulse response를 구할 수 있음.
또한, convolution에서 commutative law가 성립하므로 다음과 같이 subsystem 간의 순서가 바뀌어도 최종 system은 같음.
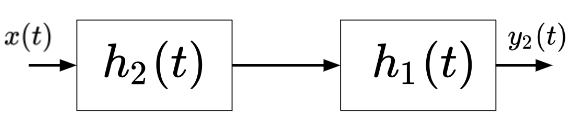
이처럼 subsystems을 연결할 경우, Cascade connection (직렬연결)이라고 하며 feed forward connection의 한 종류임(signal의 흐름이 입력에 출력으로 한 방향뿐일 경우 feed forward라고 부름).
여기서 다룬 모든 system들은 linear time invariant system임.
convolution과 impulse repsonse를 가지고 output을 구하는 것
자체가 이를 기반으로 이루어짐을 기억할 것.
728x90
'... > Signals and Systems' 카테고리의 다른 글
| [SS] Feedback Connection (0) | 2023.08.22 |
|---|---|
| [SS] Parallel Connection (1) | 2023.08.22 |
| [SS] Differential Equation and Responses (zero-input, zero-state, natural, forced) w/o Laplace Transform (0) | 2023.08.22 |
| [SS] Differential Equation and Response (zero-input, zero-state, natural, forced) w/ Laplace Transform (0) | 2023.08.22 |
| [SS] Differential Equation : 1st Canonical Form (0) | 2023.08.22 |