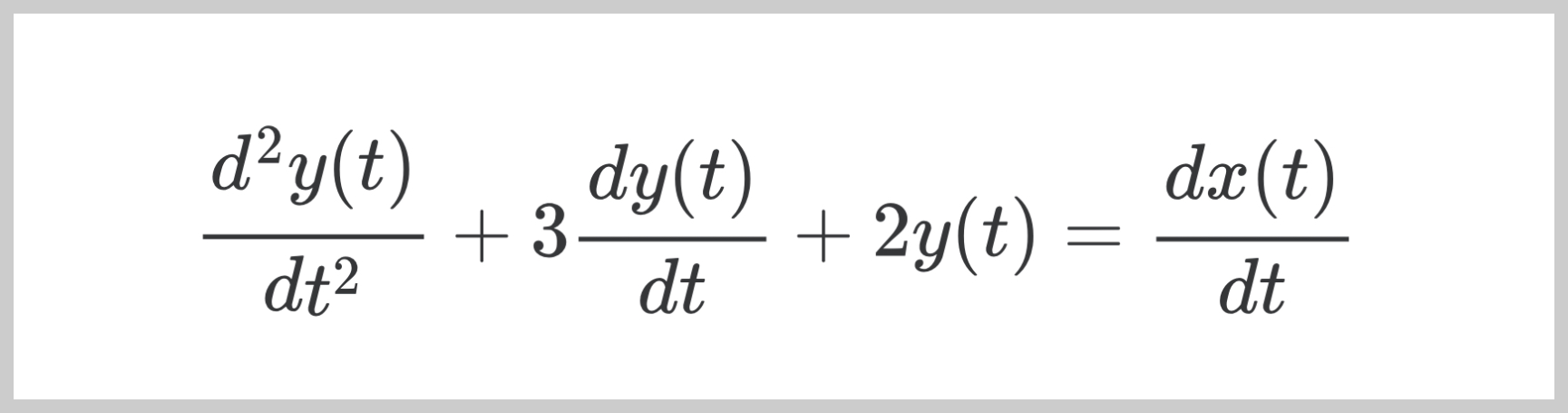
Laplace Transform을 이용한 Differential Equation을 풀기.
문제
다음 미분방정식 의 시스템이 있다고 하자.
$$
\frac{d^2 y(t)}{dt^2} + 3\frac{dy(t)}{dt}+2y(t)=\frac{dx(t)}{dt}
$$
아래와 같은 입력과 초기조건에서
- zero-state response (초기조건이 0.)
- zero-input response (input이 0.)
- natural response (system mode만으로 구성.)
- forced response (input signal에만 의한 항으로 구성.)
를 구하라.
input signal
$$
x(t)=t^2+5t
$$
initial conditions
$$
y(0^-)=2 \\
\frac{dy(0^-)}{dt} = 3
$$
sol.
우선, 시스템을 나타내는 미분방정식을 Laplace trasnform 수행함(초기조건 대입도 수행.)
$$ \begin {aligned} \frac{d^2 y(t)}{dt^2} + 3\frac{dy(t)}{dt}+2y(t) &=\frac{dx(t)}{dt} \\ \left [s^2Y(s)-sy(0)-\frac{dy(0)}{dt} \right]+ 3 \left [sY(s)-y(0) \right]+2Y(s) &= \left[ sX(s)-x(0) \right] \\ \left [s^2Y(s)-2s-3 \right]+ 3 \left [sY(s)-2 \right]+2Y(s) &= \left[ sX(s)-x(0) \right] \\ \left ( s^2+3s+2\right )Y(s)-2s-3-6&=sX(s)-0\\ \left ( s^2+3s+2\right )Y(s) &= 2s+9+sX(s)\\ Y(s) &= \frac{2s+9}{s^2+3s+2} + \frac{sX(s)}{s^2+3s+2} \end {aligned} $$
위 식에서 첫번째 항은 zero-input response에 해당하고, 두번째 항은 zero-state response에 해당함.
이제 input signal $x(t)$에 대한 Laplace transform $X(s)$를 구한다.
$$ \begin {aligned} x(t) &= t^2+5t \\ X(s) &= \frac{2!}{s^3}+5\frac{1!}{s^2} \\ &= \frac{5s+2}{s^3} \end {aligned} $$
$X(s)$를 시스템의 미분방정식의 Laplace transform에 대입한다.
$$ \begin {aligned} Y(s) &= \frac{2s+9}{s^2+3s+2} + \frac{sX(s)}{s^2+3s+2} \\ &= \frac{2s+9}{s^2+3s+2} + \frac{s(5s+2)}{s^3(s^2+3s+2)} \\ &= \frac{2s+9}{s^2+3s+2} + \frac{(5s+2)}{s^2(s^2+3s+2)}\\ &= \frac{2s+9}{(s+1)(s+2)} + \frac{(5s+2)}{s^2(s+1)(s+2)} \end {aligned} $$
이를 부분분수 분해한다.
$$ \begin {aligned} Y(s) &= \left[\frac{2s+9}{(s+1)(s+2)}\right] + \left[\frac{(5s+2)}{s^2(s+1)(s+2)}\right]\\ &= \left[\frac{A}{s+1}+\frac{B}{s+2}\right]+\left[\frac{C_1}{s^2}+\frac{C_2}{s}+\frac{D}{s+1}+\frac{E}{s+2}\right]\\ &= \left[Y_{zi}(s)\right]+\left[Y_{zs}(s)\right] \end {aligned} $$
각 부분분수의 계수를 구한다.
$$ \begin {aligned} A&=(s+1)Y_{zi}(s)\left.\right|_{s=-1}\\ &=\frac{-2+9}{(-1+2)}\\ &=7 \\ B&=(s+2)Y_{zi}(s)\left.\right|_{s=-2}\\ &=\frac{-4+9}{-2+1}\\ &=-5 \\ C_1 &=s^2Y_{zs}(s)\left.\right|_{s=0}\\ &=\frac{5\cdot0+2}{(0+1)(0+2)}\\ &=\frac{2}{2}=1 \\ C_2 &=\frac{ds^2Y_{zs}(s)}{ds}\left.\right|_{s=0} \\ &=\frac{d \left [ s^2\frac{5s+2}{S^2(s+1)(s+2)}\right]}{ds}\left.\right|_{s=0}\\ &=\frac{d \left [ s^2\frac{5s+2}{S^2(s^2+3s+2)}\right]}{ds}\left.\right|_{s=0}\\ &=\frac{5(s^2+3s+2)-(5s+2)(2s+3)}{(s^2+3s+2)^2}\left.\right|_{s=0} \\ &=\frac{5(2)-(2)(3)}{(2)^2}\\ &=\frac{10-6}{4}\\ &=1 \\ D &= (s+1)Y_{zs}(s)\left.\right|_{s=-1}\\ &=\frac{(5\cdot-1+2)}{(-1)^2(-1+2)}\\ &=\frac{-3}{1} = -3 \\ E &= (s+2)Y_{zs}(s)\left.\right|_{s=-2}\\ &=\frac{(5\cdot-2+2)}{(-2)^2(-2+1)}\\ &=\frac{-8}{-4} = 2\\ \end {aligned} $$
결국, $Y(s)$는 다음과 같음.
$$ \begin {aligned} Y(s)= \left[ \frac{7}{s+1}+\frac{-5}{s+2}\right]+\left[ \frac{1}{s^2}+\frac{1}{s}+\frac{-3}{s+1}+\frac{2}{s+2}\right] \end {aligned} $$
이들 각각에 Inverse Laplace Transform을 취한다.
$$ \begin {aligned} Y(s)&= \left[ \frac{7}{s+1}+\frac{-5}{s+2}\right]+\left[ \frac{1}{s^2}+\frac{1}{s}+\frac{-3}{s+1}+\frac{2}{s+2}\right] \\ y(t)&=\left[ 7e^{-t}-5e^{-2t}\right]+\left[ t+1-3e^{-t}+2e^{-2t}\right] \end {aligned} $$
즉, zero-input response $y_{zi}(t)$와 zero-state response $y_{zs}(t)$는 다음과 같음.
$$ \begin {aligned} y_{zi}(t)&=7e^{-t}-5e^{-2t} \\ y_{zs}(t)&=t+1-3e^{-t}+2e^{-2t} \end {aligned} $$
그리고, natural response $y_n(t)$와 forced response $y_f(t)$는 다음과 같음.
$$ \begin {aligned} y_{n}(t)&=7e^{-t}-5e^{-2t}-3e^{-t}+2e^{-2t} \\ &= 4e^{-t}-3e^{-2t}\\ y_{f}(t)&=t+1 \end {aligned} $$
같이 보면 좋은 자료
[SS] Differential Equation and Responses (zero-input, zero-state, natural, forced) w/o Laplace Transform
문제다음 미분방정식 의 시스템이 있다고 하자$$ \frac{d^2 y(t)}{dt^2} + 3\frac{dy(t)}{dt}+2y(t)=\frac{dx(t)}{dt} $$ 아래와 같은 입력과 초기조건에서zero-state response (초기조건이 0.)zero-input response (input이 0.)natur
dsaint31.tistory.com
2023.10.02 - [.../Signals and Systems] - [SS] System Response
[SS] System Response
System의 Response는 다음과 같이 3가지 기준으로 분류할 수 있음.Zero-input response vs. Zero-state response "누가 response를 만드는가? (초기조건 vs. 외부입력)" 를 기준으로 분류하는 방식이며 다음과 같은 2가
dsaint31.tistory.com
2023.08.22 - [.../Signals and Systems] - [SS] RLC Circuit & Differential Eq
[SS] RLC Circuit & Differential Eq
다음의 RLC회로를 미분방정식으로 풀기 위의 회로에서 입출력 및 초기조건은 다음과 같음. input : $x(t) = 10e^{-3t}u(t)$ (voltage) output : $y(t)$ (current) initial condition : $y(0)=0$, $V_c(0)=5$ $u(t)$ : unit step function.
dsaint31.tistory.com
'... > Signals and Systems' 카테고리의 다른 글
| [SS] Cascade Connection (0) | 2023.08.22 |
|---|---|
| [SS] Differential Equation and Responses (zero-input, zero-state, natural, forced) w/o Laplace Transform (0) | 2023.08.22 |
| [SS] Differential Equation : 1st Canonical Form (0) | 2023.08.22 |
| [SS] RLC Circuit & Differential Eq (0) | 2023.08.22 |
| [SS] Differential Equation : 2nd Canonical Form (0) | 2023.08.22 |
