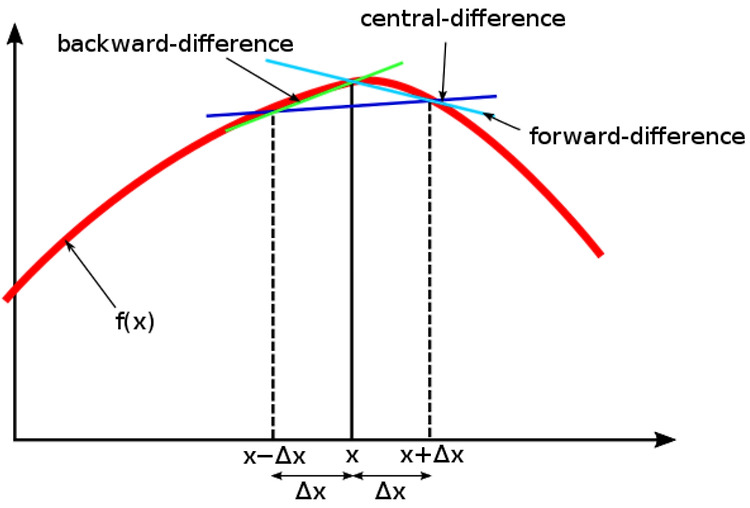
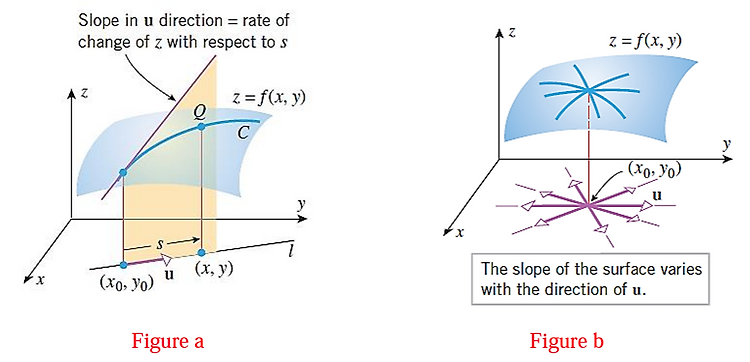
정의Function $f:\mathbb{R}^n\to \mathbb{R}$에 대해서unit vector $\textbf{u}=\begin{bmatrix}u_1 & \cdots & u_n\end{bmatrix}^\top$의 방향으로function $f$의 순간변화율이 바로 Directional Derivative임.수식$$\nabla_{\textbf{u}}f(\textbf{x})=\underset{h \to 0}{\lim}\frac{f(\textbf{x}+h\textbf{u})-f(\textbf{x})}{h}=\frac{\partial f(\textbf{x})}{\partial \textbf{u}}$$ Directional Derivative에서 방향을 결정하기 위해서 unit vector $\textbf..

Multi-Variate Function (or Scalar Field, Multi-Variable Function)에서는 Input Variable이 여러개, 즉, input이 vector이기 때문에 각각의 input variable의 변화량에 따라 output이 어떻게 변화하는지를 고려하여Derivative (도함수)를 구해야함. 이를 고려하여 하나의 input variable을 기준으로 미분을 수행한 것이 바로 Pratial Derivative임.- 이들을 모아서 column vector로 표기한 것을 Gradient라고 하며, - 이들을 row vector로 표기한 것을 1st order derivative에 해당하는 Jacobian 이라고도 부름: 차이는 - Gradient는 일반적으로 항상 (..

Derivative 란?"Differential을 구한다(Differentiation, 미분하다)" 는 derivative(도함수)를 구하는 것을 가르킴. Derivative(도함수)는average rate of change (평균변화율)의 limit인instantaneous rate of change (=derivative value, differential coefficient)(순간변화율◀ linear approximation의 slope)임.$$\displaystyle \dfrac{dy}{dx}=y^\prime=\lim_{\Delta x \to 0}\dfrac{f(x+\Delta x)-f(x)}{\Delta x}=\lim_{\Delta x \to 0}\dfrac{\Delta f(x)}{\Delta..

Differentiability $\textbf{f}:\mathbb{R}^n \to \mathbb{R}^m$ 이고, $\textbf{a} \in \mathbb{R}^n$이면서 $\textbf{f}$의 domain에 속한다고 하자. 이 때 $$ \underset{\textbf{x}\to\textbf{a}}{\lim} \frac{\textbf{f}(\textbf{x})-\textbf{f}(\textbf{a})-\textbf{L}\langle \textbf{x}-\textbf{a}\rangle}{||\textbf{x}-\textbf{a}||_2}=\textbf{0} $$ $||\textbf{x}-\textbf{a}||_2$ : $\textbf{x}$와 $\textbf{a}$의 difference vector의..

Continuity (연속) 이란If $S\subseteq \mathbb{R}^n$, then a function $f:S\to \mathbb{R}$ is continuous at $\textbf{a} \in S$ if$$\begin{equation}\label{cont.def}\forall \varepsilon >0, \ \ \exists \delta>0 \mbox{ such that if } \mathbf x \in S \mbox{ and } |\mathbf x - \mathbf a|\end{equation}$$ 만약 $f$가 모든 $S$의 point에서 continuous하다면, $f$ 는 연속함수(continuous function)임.2024.02.27 - [.../Math] - [Math] i..

1. Limit LawsAssume that $S\subseteq \mathbb{R}^n$ and that $\textbf{a}$ is a point in $\mathbb{R}^n$ is a limit point of $S$ (for example, an interior point of $S$). Further assume that $f,g:S\to \mathbb{R}$ are functions and $L$,$M$ are numbers such that$$\lim_{\mathbf x \to \mathbf a}f(\mathbf x) = L,\qquad\lim_{\mathbf x \to \mathbf a}g(\mathbf x) = M.$$ Then$$\lim_{\textbf x \to \textbf a}[..