Multi-Variate Function (or Scalar Field, Multi-Variable Function)에서는
Input Variable이 여러개, 즉, input이 vector이기 때문에
각각의 input variable의 변화량에 따라 output이 어떻게 변화하는지를 고려하여
Derivative (도함수)를 구해야함.
이를 고려하여 하나의 input variable을 기준으로 미분을 수행한 것이
바로 Partial Derivative임.
- 이들을 모아서 column vector로 표기한 것을 Gradient라고 하며,
- 이들을 row vector로 표기한 것을 1st order derivative에 해당하는 Jacobian 이라고도 부름:
차이는
- Gradient는 일반적으로 항상 (column) vector인 반면,
- Jacobian은 일반적으로 matrix인데,
- multi-variate (scalar valued) function에 대해선 특별히 1개의 row만을 가지게 되어 row vector로 표기됨.
주의: 이 박스의 내용은 numerator layout convention으로 vector calculus를 수행했을 때의 애기임.
- Partial Derivative 각각은 결국 Scalar이며 이들이 모여 Vector 이룸: (참고로 Directional Derivative도 역시 Scalar).
- 각 Variable로 기준으로 Partial Derivative를 구할 때, 나머지 Variable들은 Constant로 취급함.
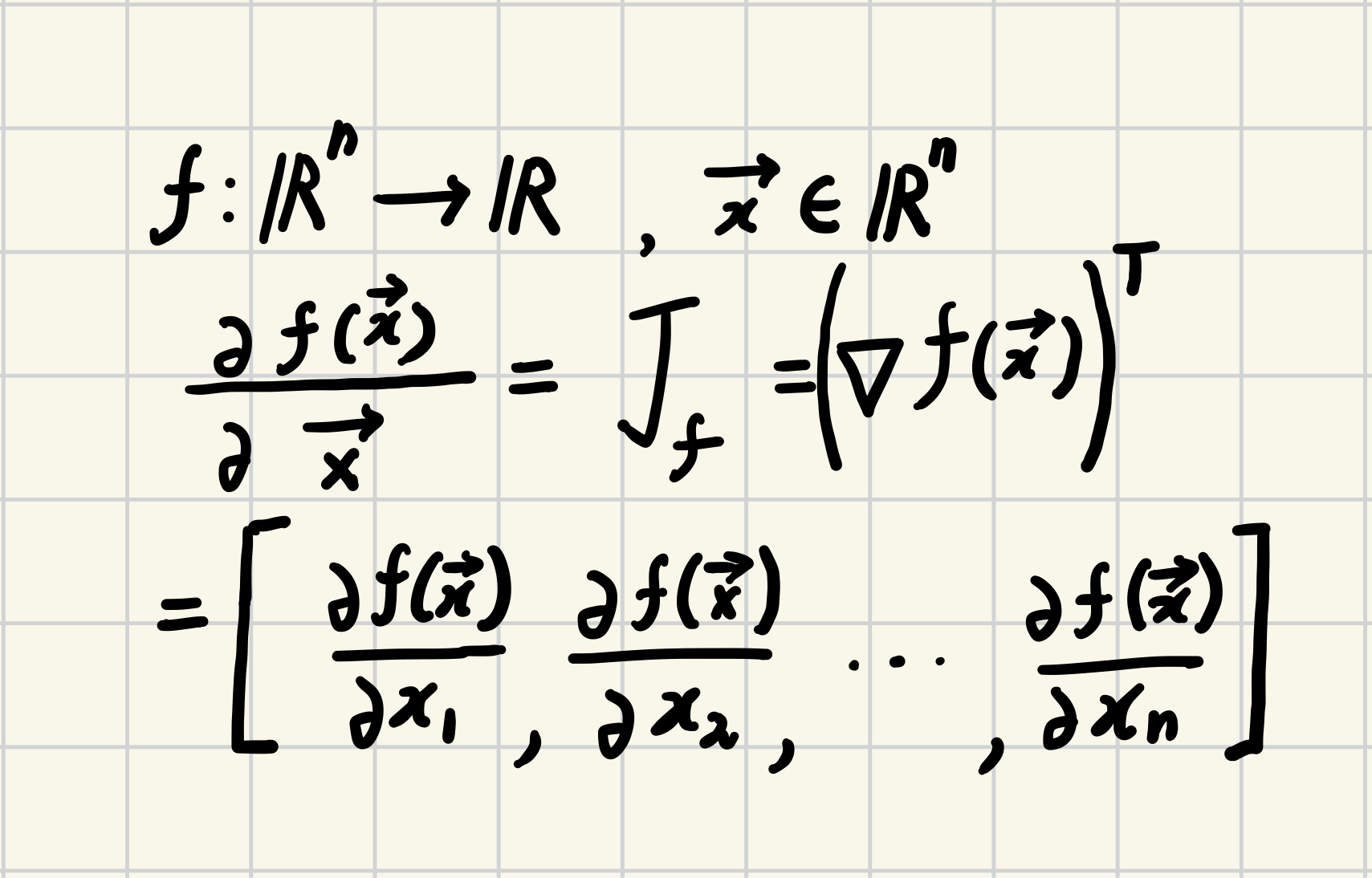
표기법
Ordinary Derivative와 구별하기 위해 Round $\partial$를 이용하여 표기함.
$$\frac{\partial f (\textbf{x})}{\partial x_i} = \underset{\Delta x \to 0}{\lim}\frac{f(x_1, \cdots, x_i + \Delta x, \cdots, x_n)- f(x_1, \cdots,x_i, \cdots, x_n)}{\Delta x}$$
참고 : Derivative of Scalar Field (=Jacobian of Scalar Field).
Multi-variate function $f$ (=Multi-Variable Function)의 경우,
- input이 vector이고 output이 scalar이므로
- $f:\mathbb{R}^n \to \mathbb{R}$로 표기된다.
다음과 같이
- input vector $\textbf{x}$를 사용하여
- 이 $f$의 partial derivatve들을 결과를 묶어서 기재할 수 도 있다.
$$\frac{\partial f(\textbf{x})}{\partial \textbf{x}}=\begin{bmatrix} \frac{\partial f}{\partial x_1} & \cdots & \frac{\partial f}{\partial x_n}\end{bmatrix}=J_{f(\textbf{x})}=J_f=\left[\nabla f(\textbf{x})\right]^T$$
- vector calculus의 경우, numerator layout convention과 denominator layout convention 등의 여러 표기법이 있음 (미분 표기에서 결과를 분자 중심으로 기재할지, 또는 분모 기준으로 기재할지의 차이가 있음.)
- 위의 예는 numerator layout convention을 따름.
- $f:\textbf{R}^n\to \textbf{R}^m$ 에서 1st order derivative가 Jacobian임.
- Scalar field의 경우, $m=1$인 경우이며 위의 Derivative가 바로 Jacobian에 해당함 (Row Vector와 동일).
- Gradient는 이 Jacobian의 transpose 임.
https://dsaint31.tistory.com/entry/Math-Summary-Jacobian
[Math] Jacobian : Summary
이 문서는 Numerator Layout Convention을 따름. Jacobian은 vector field (or multi-variate vector-valued function)에 대한 1st order derivative에 해당함. input과 output이 vector인 vector function(←vector field, $\textbf{f}:\mathbb{R}^n\to\m
dsaint31.tistory.com
Example
$$\textbf{x}=\begin{bmatrix}x_1\\x_2\end{bmatrix}, f(\textbf{x})=x_1^3+2x_1x_2^2-4x_2^2$$
위에 대한 Partial Derivative 들을 구하시오.
sol.
$\textbf{x}$의 각 축에 대해서 partial derivative들이 구해짐 (각각의 결과는 scalar)
- $\frac{\partial f(\textbf{x})}{\partial x_1} = 3x_1^22x_2^2$
- $\frac{\partial f(\textbf{x})}{\partial x_2} = 4x_1x_2-8x_2$
추가적으로 이들을 모아 vector (or matrix)로 표현한 1st order dervative인 Jacobian은 다음과 같음.
$$J_{f(\textbf{x})}=\begin{bmatrix}3x_1^2+2x_2^2 & 4x_1x_2-8x_2\end{bmatrix}$$
참고로, numeartor layout에서는 scalar field의 derivative는 row vector이고, gradient의 경우는 column vector임.
$$\nabla f (\textbf{x})= \left( J_{f(\textbf{x})} \right)^T$$
References
https://dsaint31.github.io/math/math-week03/
[Math] Week 03
Limit and Continuity
dsaint31.github.io
'... > Math' 카테고리의 다른 글
| [Math] Gradient (구배, 기울기, 경사, 경도) Vector (0) | 2023.06.24 |
|---|---|
| [Math] Directional Derivative (방향도함수) (0) | 2023.06.23 |
| [Math] Differentiation (or Differential, 미분)과 Difference (차분) (0) | 2023.06.23 |
| [Math] Differentiability of MultivariableFunctions (0) | 2023.06.23 |
| [Math] Continuity (of Multivariable Function) and Contiguity (0) | 2023.06.22 |