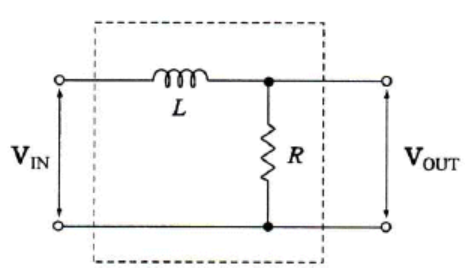
[SS] RL Circuit : differential equation 으로 풀기.
·
.../Signals and Systems
다음의 RL회로를 미분방정식으로 풀기 $t=0$에서 스위치가 닫힘. 위의 회로에서 입출력 및 초기조건은 다음과 같음. input : $E$ (voltage) output : $i(t)$ (current) initial condition : $i(t=0)=i_0=0$ (inductor L의 $t=0$에서의 전류.) 1. Differential Equation KVL에 의하여 다음이 성립 $$\begin{aligned} L\frac{di(t)}{dt}+Ri(t) &= E \\ \frac{di(t)}{dt}+\frac{R}{L}i(t) &= \frac{E}{L} \end{aligned}$$ 2. Homogeneous solution $$\begin{aligned} \frac{di_h(t)}{dt}+\frac{..