System의 impulse response는 다음을 의미한다.
System의 input이 impluse signal인 경우의
output을 해당 system의 impulse response라고 한다.
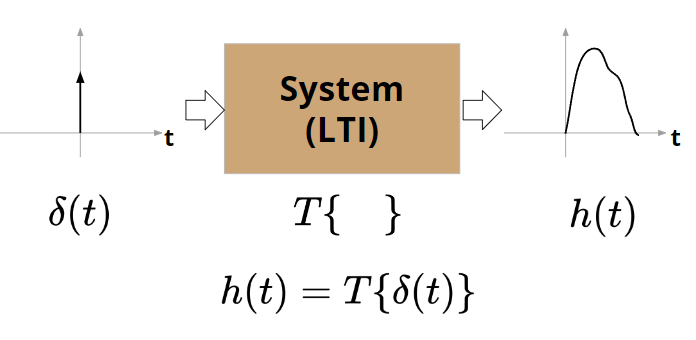
LTI system에서 출력(정확히는 zero-state response)은 impulse response와 input signal의 convolution으로 표현 가능.
LTI System에서의 Impulse response의 의미.
LTI System의 impulse response를 파악했다면 다음이 성립함.
- System의 동작을 이해함. (정확히는 initial condition이 0인 경우의)
- System의 output 생성 메카니즘을 알 수 있음.
- 임의의 input signal과 impulse response의 convolution을 통해 해당 입력에 대한 zero-state response 를 구할 수 있음.
때문에 LTI (Linear Time-Invariant or Linear Shift-Invariant) System 에 대한 해석은
결국, 해당 System의 impulse response를 정의하는 것이라고 볼 수 있음.
참고
- LTI System을 Differential Eq. 로 나타낼 경우,
- impulse response를 통해 $t=0^{-}$에서의 모든 초기조건이 0인 경우에 대한 출력 $y_{h}(t)$를 구할 수 있음
- t>0 의 zero-state (zero-IC) response).
- particular solution $y_{p}(t)$와 complete solution은 초기조건과 input이 주어져야 구할 수 있음.
- LTI System의 system mode들의 linear combination으로 impulse reponse는 이루어짐.
- Impulse Response는 엄밀하게 애기하면 “초기조건=0인 homogeneous solution”과는 다르고, “임펄스가 만든 jump 조건을 반영한 homogeneous form이라고 보면 됨: t=0에서 homogeneous solution과 차이가 발생 (impulse로 인한 jump가 일종의 초기조건처럼 동작)
예제 1.
다음과 같이 2개의 impulse function의 linear combination이 input으로 LTI System에 주어졌다고 하자.
$$ x(t)=0.5 \delta (t) + 1.2 \delta(t-1) $$
해당 LTI System의 impulse response를 $h(t)$라고 할 경우, 출력은 다음과 같음.
$$\begin{aligned} y(t) &= T\{ x(t) \} \\ &= T\{ 0.5 \delta (t) + 1.2 \delta(t-1) \} \\ &= T\{0.5\delta(t)\} + T\{1.2\delta(t-1)\} & \text{addivity} \\ &= 0.5T\{\delta(t)\} + 1.2T\{\delta(t-1)\} & \text{homogenity} \\ &= 0.5 h(t) + 1.2 h(t-1) & \text{time invariant} \end{aligned}$$
예제 2: impulser response vs. homogeneous solution (zero input, zero IC)
$$\frac{dy(t)}{dt} + a y(t) = x(t), a>0$$
2-1. Homogeneous Sol. (zero-input response) w/ zero IC (=zero Initial condition. zeor IC)
2-1-1. condition(조건):
- zero-input response w/ zero intial condition
- $x(t)=0, y(0^{-})=0$
2-1-2. solution:
$$y(t) = C e^{-at}$$
$y(0^{-})=y(0)=0 \rightarrow C=0$ 이므로, $y_h(t) = 0$임: trivial solution.
2-2. Impulser Resoponse
2-2-1. condition(조건):
- $x(t)=\delta(t), y(0^{-})=0$
2-2-2. solution:
$$\frac{d}{dt}(e^{at}y(t)) = e^{at}\delta(t) \\ \int^{0^{+}}_{0^{-}}\frac{d}{dt}e^{at}y(t))dt = \int^{0^{+}}_{0^{-}} e^{at}\delta(t)dt \\ e^{a\cdot 0}y(0^{+}) - e^{a\cdot 0}y(0^-) = e^{a\cdot 0} \int^{0^{+}}_{0^{-}}\delta(t)dt \\ y^{0^{+}} - y^{0^{-}} = 1 \\ y(0^{+})=1$$
- integrating factor method (1차 선형 ODE에 적당한 함수를 곱해 left side를 완전 도함수 꼴로 바꾸는 방법) 사용.
단, $t>0$인 경우엔 homogeneous solution과 같은 형태.
$$y(t)=C e^{-at} \\ y(0)=1=C e^{a\cdot 0} \\ \therefore y(t)=e^{at}, t>0$$
2-3. 결론
즉, Impulse Response는 zero-input response ($x(t)=0$)이면서 zero initial condition ($y(0^{-})=0$) 인 homogenesou solution의 형태이나 같은 건 아님.
- Impulse response ≠ Zero-IC homogeneous solution
- Impulse response = homogeneous form + impulse가 만든 jump 조건 반영
| Input | init. condition | solution ($t>0$) | $t=0$ | |
| Homogeneous (zero IC) | $x(t)=0$ | $y(0^-)=0$ | $y(t)=0\cdot e^{-at}=0$ | 연속, 값 = 0 |
| Impulse Response | $x(t)=\delta(t)$ | $y(0^-)=0$ | $y(t)=e^{-at}$ | $y(0^-)=0 \to y(0^+)=1$ (jump) |
같이 보면 좋은 자료
2023.10.02 - [.../Signals and Systems] - [SS] System Response
[SS] System Response
System의 Response는 다음과 같이 3가지 기준으로 분류할 수 있음.Zero-input response vs. Zero-state response "누가 response를 만드는가? (초기조건 vs. 외부입력)" 를 기준으로 분류하는 방식이며 다음과 같은 2가
dsaint31.tistory.com
'... > Signals and Systems' 카테고리의 다른 글
| [SS] System Response (1) | 2023.10.02 |
|---|---|
| [SS] System 표현하기 : Impulse Response vs. Differential Equation (1) | 2023.10.02 |
| [SS] Complex Exponential Signals (0) | 2023.09.19 |
| [SS] 주기 신호의 합에서의 주기 (Period) (0) | 2023.09.07 |
| [SS] Symmetric Signals (0) | 2023.09.07 |