[SS] Convolution with an shifted impulse

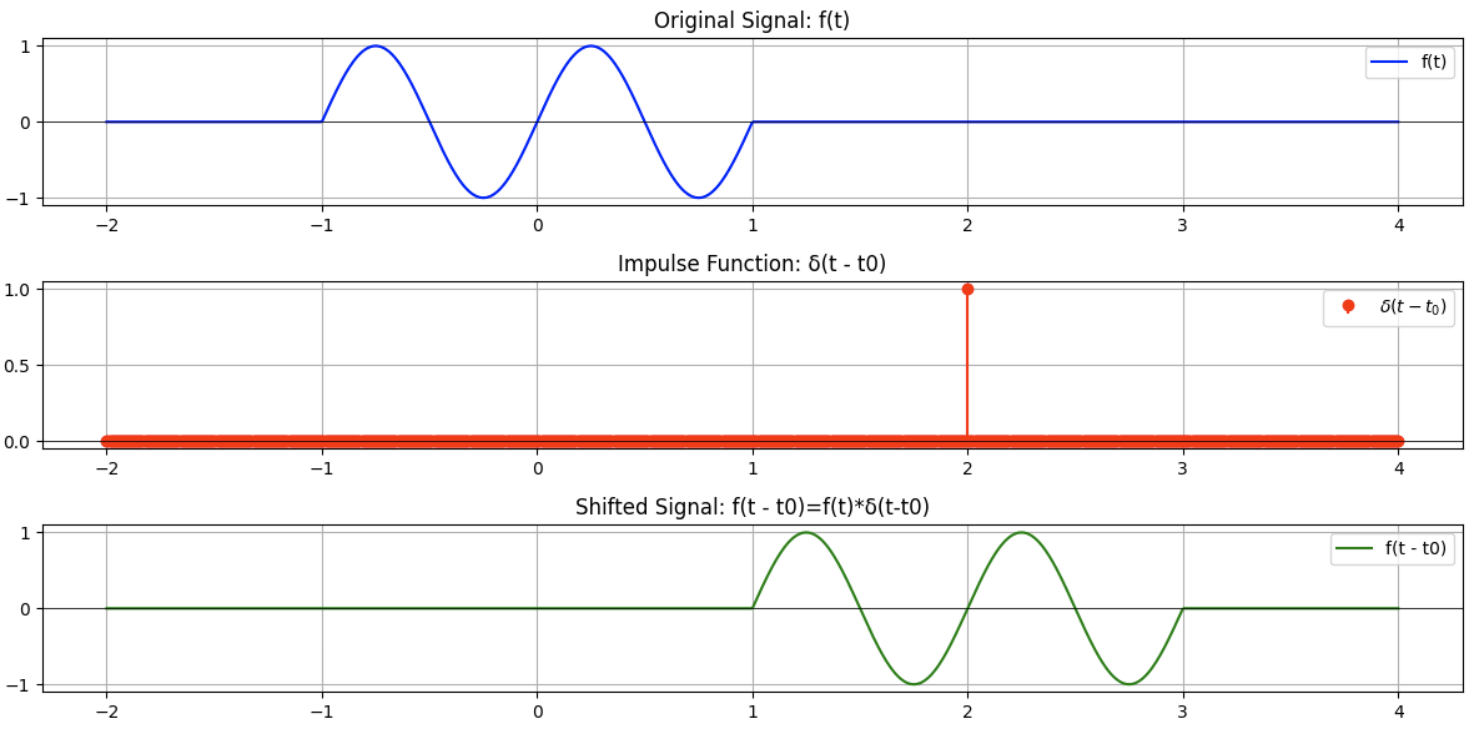
0. shifted impulse와 convolution은 결국 shifting 연산임

$t_0$로 shifting을 시킨 impulse function $\delta(t-t_0)$과의 convolution은

결국 같은 $t_0$만큼 signal을 shifting하는 것으로 볼 수 있음.

$$f(t)*\delta(t-t_0) = f(t-t_0)$$

• $*$ : convolution

---

1. 증명

$$ \begin{aligned} f(t)* g(t) &= \int^\infty_{-\infty} f(t-\color{red}{\tau}) g(\tau) d \tau \\ f(t)* \delta(t-t_0) &= \int^\infty_{-\infty} f(t-\tau) \delta(\tau - t_0) d \tau \\ &= \int^\infty_{-\infty} f(t-\color{red}{t_0}) \delta (\tau - t_0) d \tau \\ &= f(t-t_0) \end{aligned}$$

3번째 line에서 $\tau=t_0$ 일 때에 impulse function이 값을 가지므로 $f(t-\tau)=f(t-t_0)$을 고려해주면 된다.

 

convolution $*$이 commutative 이므로(교환법칙이 성립), 다음과 같이 증명할 수도 있음.

 

$$ \begin{aligned} f(t)* g(t) &= \int^\infty_{-\infty} f(\tau) g(t-\tau) d \tau \\ f(t)* \delta(t-t_0) &= \int^\infty_{-\infty} f(\color{red}{\tau}) \delta(t - t_0 - \tau) d \tau \\ &= \int^\infty_{-\infty} f(\color{red}{t-t_0}) \delta (t - t_0 - \tau) d \tau \\ &= f(t-t_0) \end{aligned}$$

3번째 line에서 $\tau=t-t_0$ 일 때에 impulse function이 값을 가지므로 $f(\tau)=f(t-t_0)$만을 고려해주면 된다.

---

2.같이 보면 좋은 자료들

2023.11.30 - [분류 전체보기] - [SS] Discrete Time Fourier Transform (DTFT) and Discrete Fourier Transform (DFT)

[SS] Discrete Time Fourier Transform (DTFT) and Discrete Fourier Transform (DFT)

---