Continuous Time Signal에서의 Impulse Function은 Dirac Delta Function $\delta(t)$임.
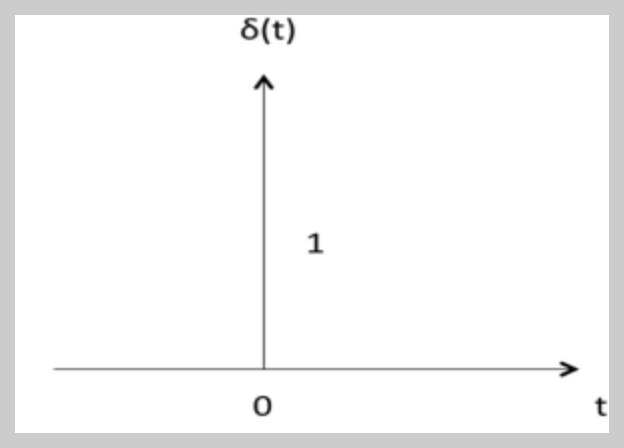
이는 다음을 만족함.
$$\delta(t)=\left\{ \begin{matrix} \infty &,t=0 \\ 0 &,t \ne 0 \end{matrix}\right. \\ \int^\infty_{-\infty} \delta(t)dt=1$$
2022.08.29 - [.../Signals and Systems] - [SS] Impulse Function (Dirac Delta Function)
[SS] Impulse Function (Dirac Delta Function)
다음과 같이 정의 되는 함수를 $\delta_\epsilon(t)$라고 하자. $$\delta_\epsilon( t ) =\left\{ \begin{matrix} 0 & ,t < -\frac { \varepsilon }{ 2 } \\ \frac { 1 }{ \varepsilon } & ,-\frac { \varepsilon }{ 2 } \le t
dsaint31.tistory.com
Fourier Transform은 위의 impulse function의 성질을 이용하여 쉽게 다음과 같이 구해짐.
$$\begin{aligned} \mathcal{F}\left[ \delta (t) \right] &= \int^\infty_{-\infty} \delta(t) e^{-j\Omega t}dt \\ &= \int^\infty_{-\infty} \delta(t) e^{-j\Omega \color{red}{0} } dt \\ &= e^{-j\Omega \color{red}{0} } \int^\infty_{-\infty} \delta(t) dt \\ &= 1 \end{aligned}$$
읽어보면 좋은 자료
2023.08.21 - [.../Signals and Systems] - [SS] Properties of Impulse Function
[SS] Properties of Impulse Function
Impulse function (or Dirac delta function)은 이상적으로, 오직 한 점에서만 무한대의 값을 가지고,나머지에서는 0의 값을 가지며,적분시 면적인 1이 되는 함수 다른 function을 분석하거나, system의 response를
dsaint31.tistory.com
2023.10.13 - [.../Signals and Systems] - [SS] A Short Table : Fourier Transform
[SS] Fourier Transform Table
0. Fourier Transform Table $x(t)$$X(\omega)$ 1$e^{-a t}u(t), a>0$$\frac{1}{a+j\omega}$ref.2$e^{a t} u(-t) , a>0$$\frac{1}{a-j\omega}$ 3$e^{-a \vert t\vert}, a>0$$\frac{2a}{a^2+\omega^2}$ 4$te^{-a t}u(t), a>0$$\frac{1}{ (a+j\omega)^2}$ 5$t^ne^{-a t}u(t
dsaint31.tistory.com
'... > Signals and Systems' 카테고리의 다른 글
| [SS] Convolution with an shifted impulse (0) | 2023.10.19 |
|---|---|
| [SS] CTFT Properties : Modulation Theorem (1) | 2023.10.19 |
| [SS] Fourier Transform Table (0) | 2023.10.13 |
| [SS] 1장 관련 Quiz (1) | 2023.10.06 |
| [SS] Separable signal (1) | 2023.10.06 |