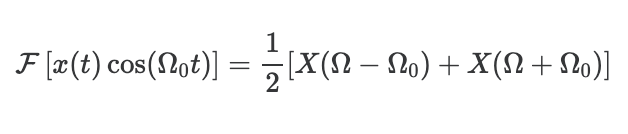
CTFT 에서 Modulation Property란
$x(t)$의 CTFT가 $X(\Omega)$인 경우,
$x(t) \cos (\Omega_0 t)$의 CTFT가 다음과 같음을 의미함.
$$\mathcal{F}\left[ x(t) \cos (\Omega_0 t)\right] = \frac{1}{2} \left[ X(\Omega-\Omega_0) + X(\Omega+\Omega_0)\right]$$
추가적으로,
$x(t) \sin (\Omega_0 t)$의 CTFT도 다음과 같이 구해짐.
$$\mathcal{F}\left[ x(t) \sin (\Omega_0 t) \right] = \frac{1}{2j} \left[ X(\Omega - \Omega_0) - X(\Omega + \Omega_0)\right]$$
증명 ($\cos$ 경우만).
CTFT에 의해 다음이 성립.
$$ \mathcal{F}\left[ x(t) \right] = X(\Omega)=\int_{−\infty}^{\infty}x(t)e^{-j\Omega t} \:dt $$
여기 $x(t) \cos (\Omega_0 t)$의 CTFT는 다음과 같음.
$$ \begin{aligned} \mathcal{F} \left[ x(t) \cos (\Omega_{0} t) \right] &= \int_{ -\infty}^{\infty}x(t) \cos (\Omega_{0} t) e^{-j\Omega t} \: dt \\ &= \int_{ -\infty}^{\infty}x(t) \left[ \frac{e^{j\Omega_0 t}+ e^{-j\Omega_0 t}}{2} \right] e^{-j \Omega t} \: dt \\ &= \frac{1}{2} \mathcal{F} \left[ x(t) e ^{j\Omega_0 t} \right] + \frac{1}{2} \mathcal{F} \left[ x(t) e ^{-j\Omega_0 t}\right] \\ &= \frac{1}{2} X(\Omega -\Omega_0) + \frac{1}{2} X(\Omega + \Omega_0) \end{aligned}$$
Signal의 Modulation
DIP등에서 사용되는 signal의 Modulation은 조금 다른 의미로 사용된다.
다음 URL을 참고할 것.
2022.09.26 - [Programming/DIP] - [DIP] Modulation Transfer Function and Contrast
[DIP] Modulation Transfer Function and Contrast
Modulation Transfer Function (MTF) MTF can be defined as the magnitude of the Fourier transform of the point or line spread function. 입력신호가 어떤 장치-시스템을 통과하고 난 후 그 물리적 특성이 어떻게 변하는지를 나타
dsaint31.tistory.com
'... > Signals and Systems' 카테고리의 다른 글
| [SS] System Representation w/ Laplace Transform (0) | 2023.11.16 |
|---|---|
| [SS] Convolution with an shifted impulse (0) | 2023.10.19 |
| [SS] Fourier Transform of Impulse Function (Dirac Delta) (0) | 2023.10.13 |
| [SS] Fourier Transform Table (0) | 2023.10.13 |
| [SS] 1장 관련 Quiz (1) | 2023.10.06 |