Scalar
- 오직 magnitude(크기)만을 가지는 물리량.
- 숫자 하나.
ndim=0,rank=0
2024.07.08 - [.../Linear Algebra] - [LA] Rank: Matrix의 속성
[LA] Rank: Matrix의 속성
Definition: Rank ◁ matrix 속성The rank of a matrix $A$, denoted by rank $A$,is the dimension of the column space of $A$.Matrix를 이루는 Column Vectors에서 Linearly Independent 인 것들의 수를 의미Row Space의 Dimension 의 경우를 강
dsaint31.tistory.com
2025.02.03 - [Programming/ML] - [ML] Tensor: Scalar, Vector, Matrix.
[ML] Tensor: Scalar, Vector, Matrix.
Tensor 종류1. Scalar (0차원 tensor)하나의 숫자로 표현되는 가장 기본적인 형태.크기(magnitude)만을 가지며 방향은 없음.예시: 온도(25°C), 나이(20), 가격(1000원)# 파이썬/NumPy에서의 표현scalar = 5.02. Vector (
dsaint31.tistory.com
Vector
- magnitude와 direction을 가지는 물리량.
- ordered list of numbers 가 가장 쉬운(?) 정의임.
- 엄밀한 정의는 Vector Space의 Element가 바로 Vector임.
ndim=1,rank=1로 vector가 표현됨. : vector는 다차원 vector space의 특정 point를 가르키는데 사용됨.
2022.04.05 - [.../Math] - [Math] Definition of Vector Space
[Math] Definition of Vector Space
Vector 의 엄밀한(?) 정의는 Vector Space의 Element임.즉, Vector를 제대로 이해하려면 Vector Space에 대한 정의를 확실히 이해해야 한다.Vector Space의 정의.Vector Space는 아래를 만족하는 Non-Empty Set을 가르킴.Ve
dsaint31.tistory.com
Zero Vector
- 모든 component(성분 or element)의 값이 0인 vector
차원 (Dimension)
- Vector의 component (or element)의 수.
- $\langle 1,2,3 \rangle$는 3차원 vector space에 속하는 요소를 나타냄.
Vector는 1차원이지만, 이를 통해 다차원 공간의 특정 element를 표현할 수 있음.
위의 $\langle 1,2,3 \rangle$은 3차원 Vector Space 의 한 element이므로 3차원 벡터이나 벡터 자체는 1차원 데이터임.
즉 1차원 데이터인 벡터는 다차원 공간의 한 element를 가리키는 데 사용가능.
전치 (Transpose)
- row와 column이 교환됨. row vector의 transpose는 column vector.
- $\vec{x}^\top = \textbf{x}^\top = \begin{bmatrix}x_1 \\ x_2 \\ x_3\end{bmatrix}^\top = \begin{bmatrix} x_1 & x_2 & x_3 \end{bmatrix}$
- $(\mathbf{xy})^\top=\mathbf{y}^\top \mathbf{x}^\top$
Norm (노름)
- vector의 length 혹은 magnitude로 불림.
- 3차원 공간에서 Euclidean Norm은 다음과 같이 정의됨.
$$| \vec{a} | =\| \vec{a} \|_2 = (a^2_1+a^2_2+a^2_3)^{\dfrac{1}{2}}$$ - 일반적인 L$p$-norm의 정의는 다음을 만족하는 것을 가르킴.
- ${ \| \vec{a} \| }_{P} \ge 0$, $ \vec{a} = \vec{0}$ 일 경우, ${ \| \vec{a} \| }_{P}=0$
- ${ \| c \vec{a} \| }_P = | c | { \| \vec{a} \| }_{P}$. 여기서 $c$는 상수. (양의 동차성)
- ${ \| \vec { a } +\vec { b } \| }_{ P }\le { \| \vec { a } \| }_{ P }+{ \| \vec { b } \| }_{ P }$ : Triangular Inequality
- $| \vec{a} \cdot \vec{b} | \le \| \vec{a} \| \| \vec{b} \|$ : Cauchy-Schwarz Inequality
- Euclidean norm의 경우 $P=2$인 경우임.
- $\|\vec{a}\|_2 = \sqrt{\vec{a}\cdot \vec{a}} = \sqrt{\vec{a}^\top\vec{a}}$
https://bme808.blogspot.com/2022/10/norm.html
Norm (노름)
Vector 및 matrix의 크기에 해당하는 양(magnitude) 을 구하는 연산 으로 사용됨. The higher the norm index($p$값이 클 경우), the more it focuses on large values ...
bme808.blogspot.com
Position Vector (위치벡터, $\vec{r}$)
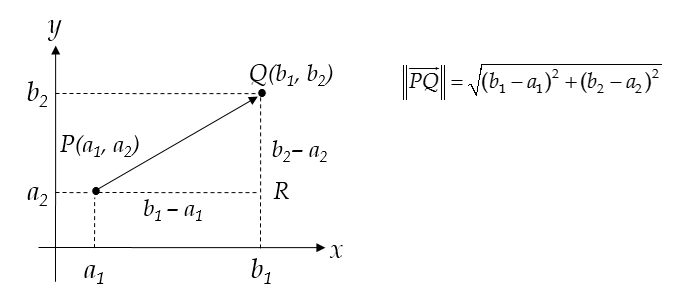
- 평면 $\mathbb{R}^2$에서 점 $P(a_1,a_2)$에서 점 $Q(b_1,b_2)$ 방향의 vector는 다음 그림과 같음.
- 여기서 $P$는 initial point(시작점,시점)이고, $Q$는 terminal point(종점)이라 함.
- position vector는 일반적으로 initial point가 원점 인 경우로서, 이 경우 terminal point $Q$의 position vector라고 불림.
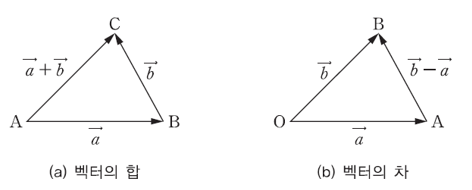
Vector의 합, 차, 상수배
- 다음의 두 vector가 있다고 하자.
$$\begin{aligned} \vec { a } &=\langle a_1 ,a_2,a_3\rangle \\
\vec { b } &= \langle b_1 ,b_2,b_3\rangle \\
\end{aligned}$$ - 합과 차, 상수배
$$\begin{aligned} \vec{a} + \vec{b} &= \langle a_1 + b_1 , a_2 + b_2 , a_3 + b_3 \rangle \\
\vec{a} - \vec{b} &= \langle a_1 - b_1 , a_2 - b_2 , a_3 - b_3 \rangle \\
c\vec{a} &= \langle ca_1, ca_2, ca_3 \rangle, c \text{ is constant.} \end{aligned}$$
Unit Vector
- $\left| \vec { a } \right| =1$인 $\vec{a}$ (or $\textbf{a}$)를 unit vector라고 함.
Normalization
- 방향은 유지하되 norm인 1인 unit vector로 만드는 것
$$
\begin{aligned}
\frac{1}{\left| \vec { a } \right| }\vec { a } \end{aligned}$$
dot product (or inner product or scalar product)
- 내적 이라고 불리는 연산으로 다음과 같이 정의되며, 결과가 scalar 임.
$$\begin{aligned}
\vec { a } \cdot \vec { b } &=|| \vec { a } || || \vec { b } | | \cos { \theta } \\ \quad & = { a }_{ 1 }{ b }_{ 1 }+{ a }_{ 2 }{ b }_{ 2 }{ +a }_{ 3 }{ b }_{ 3 } \end{aligned}$$ - Column Vector 에서는 다음으로 정의됨: $\textbf{a}^\top \textbf{b}$
- 두 vector 사이의 angle(각)을 구하는데 많이 이용됨.
- 또는 두 vector 사이의 similarity를 구하는데 많이 이용됨 : 2023.07.23 - [.../Math] - [ML] Cosine Similarity
dot 곱은 엄밀히 애기하면, inner product의 한 종류이나 ML등에서는 같은 것으로 봐도 큰 문제 없음.
https://youtu.be/zSd7jd2HGhM?si=_N19F3HeciGtHmrZ
Inner product는 Projection과 매우 관계가 깊음.
2022.05.19 - [.../Math] - [Math] Orthogonal Projection (정사영)
[Math] Orthogonal Projection (정사영)
Projection $\textbf{x}_1$ onto $\textbf{w}$ (vector $\bf{x}$를 vector $\bf{w}$에 투영) 를 수식으로 표현하면 다음과 같음. $$\text{proj}_\textbf{w}\textbf{x}=\dfrac{\bf{x}\cdot\bf{w}}{\bf{w}\cdot\bf{w}}\bf{w}=\dfrac{\bf{x}\cdot\bf{w}}{\bf{w
dsaint31.tistory.com
보다 자세한 건 다음을 참고:
2024.10.28 - [.../Math] - [Math] Inner Product (or Hermitian Inner Product, 내적)
[Math] Inner Product (or Hermitian Inner Product, 내적)
Inner product (내적)은 vectoer space이나 function space에서 두 대상 간의 relationship(관계)를 나타내는 operation(연산). 다음의 세 가지 성질을 만족할 때 Inner Product라 부르며, 이를 통해두 벡터나 함수 간의s
dsaint31.tistory.com
Outer Product
Column Vector로 이 연산을 표현하면 다음과 같음.
$$\textbf{a}\textbf{b}^\top=C$$
- $\textbf{a}, \textbf{b}$는 Column Vector.
- $C$ 는 matrix 임.
즉, Outer Product는 벡터들을 통해 Matrix가 얻어짐.
아래의 Cross Product를 국내에선 외적이라고 많이 부르는데,
Outer Product는 Cross Product와 전혀 다른 연산임.
주의할것.
Outper Product 를 이용하여 Projection Matrix를 만들기도 함.
Vector $\mathbf{x}$를 Unit Vector $\mathbf{u}$에 Projection을 수행을
다음과 같은 Matrix-Vector Mulitplication으로 표현:
$$\text{Project}_{\mathbf{u}} \mathbf{x} = \dfrac{ \mathbf{u}\mathbf{u}^\top}{\|u\|^2} \mathbf{x} = \mathbf{u}\mathbf{u}^\top \mathbf{x}$$
2022.05.19 - [.../Math] - [Math] Orthogonal Projection (정사영)
[Math] Orthogonal Projection (정사영)
Projection $\textbf{x}_1$ onto $\textbf{w}$ (vector $\bf{x}$를 vector $\bf{w}$에 투영) 를 수식으로 표현하면 다음과 같음. $$\begin{aligned}\text{proj}_\textbf{w}\textbf{x}&=\dfrac{\bf{x}\cdot\bf{w}}{\bf{w}\cdot\bf{w}}\bf{w}=\dfrac{\bf{x
dsaint31.tistory.com
Cross Product (Vector Product)
- 외적 이라고 많이 기재(일본식 용어)되는데...
이는 구분되는 다른 연산인 outer product로 오해하는 문제가 발생하기 때문에 권하지 않음. - 주로 3차원 vector에서만 사용되며, operands에 해당하는 vector 들에 직교하는 vector를 결과로 냄.
- 물리 등에서 회전, 방향 등에 관련된 문제에서 많이 사용됨.
- Linear Algebra 의 Outer Product는 결과가 Matrix로 나오며,
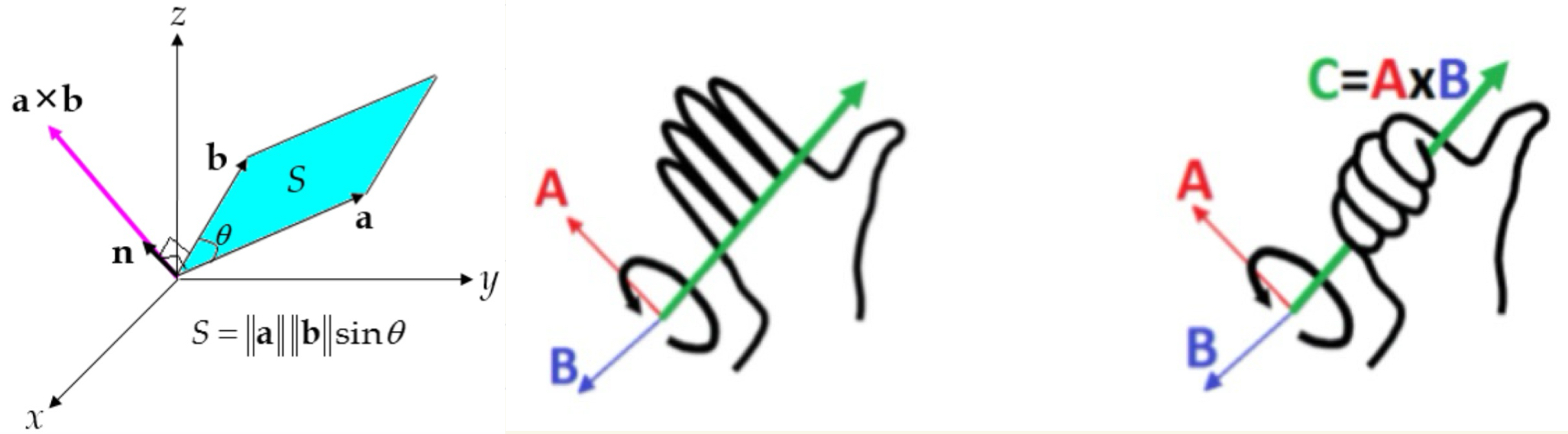
다차원 Vector를 Operand로 삼고 결과가 Vector인 Cross Product와 구분되는 다른 연산임. - 기하학적으로는 두 벡터가 이루는 평행사변형의 넓이가 Cross Product의 크기임.
- Cross Product 연산으로 다음과 같이 정의되며, 결과가 Vector 임. $$\begin {aligned}
\vec { a } \times \vec { b } &=\left( { \left| \vec { a } \right| }\left| \vec { b } \right| \sin { \theta } \right) \vec { n } \\
\quad &= \begin{vmatrix} \vec {i} & \vec {j} & \vec {k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3\end{vmatrix} \\
\quad &= \vec {i} \begin{vmatrix} a_2 & a_3 \\ b_2 & b_3 \end{vmatrix} + \vec {j} \begin{vmatrix} a_3 & a_1 \\ b_3 & b_1 \end{vmatrix} + \vec {k} \begin{vmatrix} a_1 & a_2 \\ b_1 & b_2 \end{vmatrix} \\
\quad &= \vec{i}(a_2b_3-a_3b_2)+\vec{j}(a_3b_1-a_1b_3)+\vec{k}(a_1b_2-a_2b_1)
\\ \end {aligned}$$ - Cross Product 연산을 Matrix Multiplication로 표현하기도 함: Machine Vision 에서 많이 애용됨.
- 여기서 $\vec{n}$ 은 unit normal vector이며 right hand law에 따른 방향을 가지며 $\vec{a}$ 와 $\vec{b}$ 에 orthogonal(수직)임.
Orthogonality
- $\vec{a}\ne \vec{0}$와 $\vec{b}\ne \vec{0}$가 성립하면서,
- $\vec{a}$와 $\vec{b}$의 inner product가 0일 경우,
- 이 두 vector가 orthogonal(직교)하다 라고 함.
Cartesian Coordinate System(or Rectangular Coordinate System)에서 Vector표현.
- 벡터 $\mathbf{v}$를 다음과 같은 직교좌표계에서 나타낼 경우,
$\textbf{i,j,k}$를 x축, y축, z축의 positive direction을 방향으로 하는
orthonormal vectors 들의 표기로 삼고,
이들을 basis 로 이용하여 표현.
$$
\vec{v}=a\vec{i}+b\vec{j}+c\vec{k}
$$
- Orthonormal Vector : 단위 벡터이며 서로에 대해 orthogonal이며 basis 로 사용됨.
- $\vec{i},\vec{j},\vec{k}$는 서로 orthogonal함.
- 최소한 linearly independent를 만족해야 basis로 사용가능.
2024.02.04 - [.../Math] - [Math] Cartesian Product (or Descartes Product, Product Set)
[Math] Cartesian Product (or Descartes Product, Product Set)
Cartesian Product (or Descartes Product) 공집합(empty set, null set)이 아닌 여러 sets를 이용하여 새로운 set을 만드는 연산. Cartesian product는 operand인 여러 집합들의 각 elements를 원소(component, element)로 하는 tuple
dsaint31.tistory.com
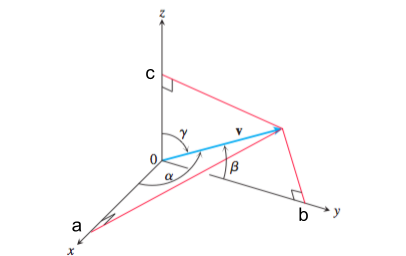
Directional cosine (방향여현) & Directional angles
- $\vec{v}$ 의 directional angles $\alpha,\beta,\gamma$는 다음과 같이 정의됨.
- $\alpha$ is the angle b/w $\vec{v}$ and the positive x-axis ($0 \le \alpha \le \pi$)
- $\beta$ is the angle b/w $\vec{v}$ and the positive y-axis ($0 \le \beta \le \pi$)
- $\gamma$ is the angle b/w $\vec{v}$ and the positive z-axis ($0 \le \gamma \le \pi$)
- $\vec{v}$의 directional cosines $\lambda, \mu, \nu$는 다음과 같이 정의됨.
- $\lambda = \cos{\alpha} = \frac{a}{\left|\vec{v}\right|}$
- $\mu = \cos{\beta} = \frac{b}{\left|\vec{v}\right|}$
- $\nu = \cos{\gamma} = \frac{c}{\left|\vec{v}\right|}$
다음이 성립함.
$$\begin{aligned}\left\|\vec {v}\right\|_2 = A = |\vec {v}| &= \sqrt{a^2+b^2+c^2}\\&=A\sqrt{\lambda^2+\mu^2+\nu^2} \\ \therefore \sqrt{\lambda^2+\mu^2+\nu^2} &= 1\\ \end{aligned}$$
같이보면 좋은 자료들
2022.03.28 - [.../Math] - [Math] Vector (2) : Vector Function
[Math] Vector (2) : Vector Function
Definition of Vector Function A vector function is simply a function whose codomain(공역) is $\mathbb{R}^n$. In other words, rather than taking on real values, it takes on vector values. We will often use the notation $\vec{v} = \vec{v}(t)$ to denote a v
dsaint31.tistory.com
2025.01.21 - [.../Linear Algebra] - [Summary] Linear Algebra (작성중)
[Summary] Linear Algebra (작성중)
ML 을 위해 Linear Algebra 공부시 참고할만한 책더보기전체적으로 공부를 한다면 다음을 권함.Linear Algebra and Its Application, 5th ed 이상, David C. Lay5th ed. 는 웹에서 쉽게 pdf도 구할 수 있음. 다음은 1~2개
dsaint31.tistory.com
'... > Math' 카테고리의 다른 글
| [Statistics] Central Limit Theorem (0) | 2022.03.31 |
|---|---|
| [Statistics] Moment (Probability Moment) (0) | 2022.03.31 |
| [Math] Vector (2) : Vector Function (0) | 2022.03.28 |
| Softplus (0) | 2022.03.14 |
| [Math] Function (함수): 간략 정의 (0) | 2021.09.14 |