Hungarian Algorithm
Hungarian Algorithm은 bipartite graph의 매칭 문제를 해결하는 데 사용됨.
Bipartite graph의 매칭 문제는 Data Association 또는 Resource Assignment Problem이라고도 불림.
두 개의 독립된 set을 연결하는 최적의 matcing을 찾기 위해
cost matrix(비용 행렬)을 이용하여 수행되는데
Hungarian Algorithm은 bipartite graph에서
모든 edge의 weight(가중치)를 minimize(최소화)하는 optimal matching을 찾음.
2024.08.06 - [Computer/CE] - [CE] Bipartite Graph (이분그래프)
[CE] Bipartite Graph (이분그래프)
Bipartite GraphNode (or Vertex)들을 edges의 구성에 따라 2개의 집합으로 나눌 수 있는 Graph. Nodes의 전체 set이 2개의 subset으로 나누어지며, 같은 subset에 속하는 node들 간에는 edge가 존재하지 않음. Graph에
dsaint31.tistory.com
Overview of Hungarian Algorithm
- cost matrix 계산함: (반드시 square matrix가 되어야 하며 아닌 경우 padding 필요)
- 각 row 에서 가장 작은 항목을 해당 row 의 다른 모든 항목에서 빼기. 이렇게 하면 row 의 가장 작은 항목이 0이 됨.
- 각 column 에서 가장 작은 항목을 해당 column 의 다른 모든 항목에서 빼기. 이렇게 하면 column 의 가장 작은 항목이 0이 됨.
- 가능한 적은 수의 lines 로 모든 0 항목을 모두 cover(커버)하도록 line 그리기.
이는 cost matrix의 모든 0을 커버하는 최소한의 row 와 column의 set 구하기 를 의미함. - 만약 그려진 lines (커버하는 최소한의 row와 column의 set의 원소)가 $N$개라면, 최적 할당이 완료된 것이므로 알고리즘 완료됨.
- 최적의 할당은 0이 위치한 자리임 (0 항목의 행과 열이 matching)
- lines의 수가 $N$보다 적으면, 최적 수의 0이 아직 달성되지 않은 것으로 다음 단계로 이동.
- 어떠한 line으로도 커버되지 않은 영역에서 가장 작은 항목 찾은 후 이 항목의 값으로 현재 커버되지 않은 영역을 가지는 모든 rows의 항목들에서 빼준다. 이후 negative(음수)가 된 항목을 포함한 columns에 대해 최소값이 0이 되도록 각 column에 더하기를 수행하고, 단계 3으로 돌아감.
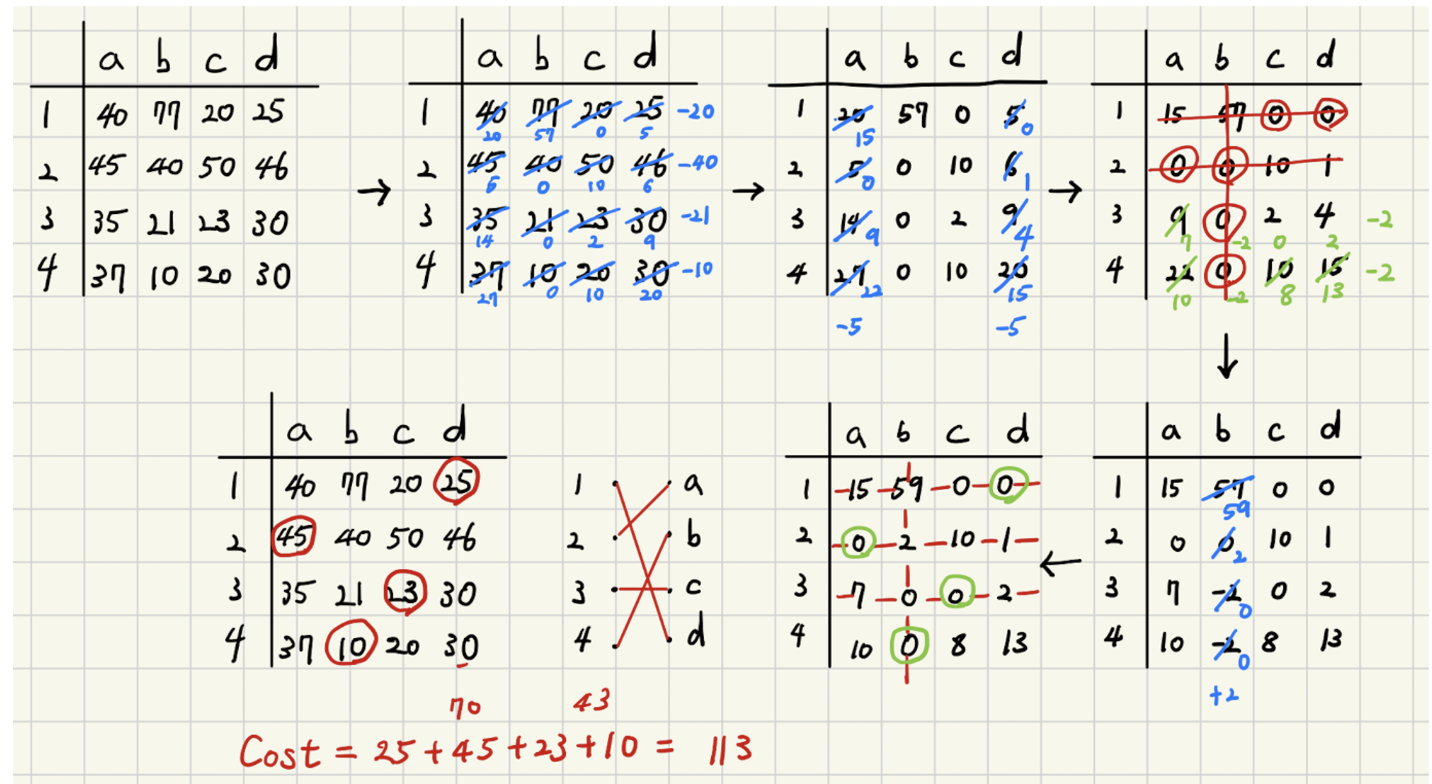
다음 예제 풀이를 참고
Square Matrix가 아닌 경우 처리.
Hungarian algorithm 은 기본적으로 cost matrix 가 square matrix 인 경우에만 동작하도록 설계되어 있으나
square matrix 아닌 경우에도 적용할 수 있음.
이를 위해 다음과 같은 과정을 거침.
- rectangle matrix을 square matrix로 변환:
- 비용 행렬이 $m \times n$ 크기 ( $m \ne n$ )라면, 더 큰 row (또는 column)에 맞춰 square matrix가 되도록 padding을 수행.
- padding 으로 추가되는 row 또는 column의 요소들은 모두 큰 값(예: 무한대)으로 채움.
- 이는 추가된 row 또는 column이 최적의 solution 을 찾는데 영향을 주지 않도록 하기 위함.
- Hungarian algorithm 적용:
- 변환된 square matrix에 Hungarian algorithm을 적용하여 최적 할당을 찾음.
- 원래 문제로 돌아오기:
- 추가된 행 또는 열에 대한 할당은 무시하고, 원래의 rectangular matrix 에 대한 최적 할당 만을 취함.
단점
Computation Complexity가 $O(N^3)$ 로 느린 편에 속함: real-time application에 적용하기 쉽지 않음.
관련 Youtubes
Object Detection (or Object Tracking)의 관점에서의 Hungarian Algorithm에 대한 설명 (간단한 편).
Object Detection Part 6: The Hungarian Matching Algorithm, Tracking, Bounding Box Matching
좀더 자세한 설명은 다음 링크를 참조.
Hungarian Algorithm
References
할당 문제 & 헝가리안 알고리즘 (Assignment Problem & Hungarian Algorithm)
할당 문제 & 헝가리안 알고리즘 (Assignment Problem & Hungarian Algorithm)
이번 포스팅에서는 assignment problem과 Hungarian algorithm에 대해서 알아보겠습니다. 먼저 assignment problem이 어떤 것인지에 대해서 살펴보고, 이를 해결하는 방법을 알아보도록 하겠습니다. 인터넷을 찾
gazelle-and-cs.tistory.com
'Programming > DIP' 카테고리의 다른 글
| [CV] DIP, Image Analysis, and Computer Vision (4) | 2024.09.01 |
|---|---|
| [CV] Ideal Pinhole Size (0) | 2024.08.09 |
| [CV] Motion Field vs. Optical Flow (0) | 2024.07.18 |
| [CV] Depth Camera (or Active Sensor): Structured Light (1) | 2024.07.18 |
| [CV] Depth Cameras (1) | 2024.07.17 |