Homogeneous Coordinates (동차 좌표)와 Projective Geometry (사영 기하학)
1. 개요
1-1. Homogeneous Coordinates의 정의와 특성
Homogeneous Coordinates (동차 좌표)는 Euclidean Coordinates (유클리드 좌표) 시스템을 확장하여 Projective Geometry (사영 기하학)에서 사용되는 좌표 시스템임.
- 이는 3차원 또는 2차원 Euclidean Space (유클리드 공간)의 점을 한 차원 더 높은 공간에서 표현하는 방법임.
- Projective Space P2는 평면(2차원)의 점을 homogeneous coordinates로 나타냄.
- P2=R3−0 로, 2차원의 point를 나타내는데 3차원의 Euclidean Space R3가 사용됨.
- Homogeneous Coordinates (동차 좌표)는 평행선이 무한히 먼 곳에서 교차하는 등의 Projective Geometry (사영 기하학)적 특성을 효과적으로 표현할 수 있음.
1-2. Homogeneous Coordinates의 확장과 변환
Homogeneous Coordinates (동차 좌표) 시스템에서는 2D Euclidean Coordinates (유클리드 좌표) (x,y)를 (x,y,w)로 확장하고, 3D Euclidean Coordinates (유클리드 좌표) (x,y,z)를 (x,y,z,w)로 확장함.
- 여기서 w 는 Scaling Factor (스케일링 인자)로, 점의 실제 위치는 (x/w,y/w) 또는 (x/w,y/w,z/w)로 계산됨.
- Homogeneous Coordinates (동차 좌표)의 중요한 특징 중 하나는 Transformation Matrix (변환 행렬)을 사용하여 기하학적 변환을 일관되게 적용할 수 있다는 점임.
- translation에 의한 비선형성을 선형으로 바꾸는데 사용된다.
- 이는 컴퓨터 그래픽스, 로보틱스, 사진 측량 등 다양한 분야에서 유용하게 사용됨.

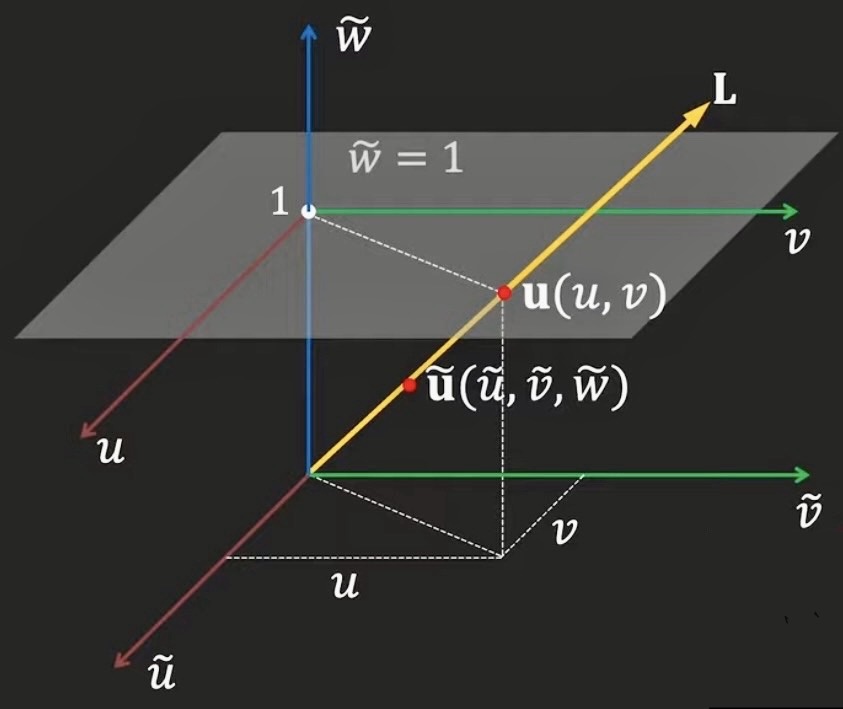
위 그림은 2차원의 점 (u,v)가 어떻게 homogeneous coordinate인 (u,v,w)에 대응되는지를 도식적으로 표현함.
위 그림에서 orign을 제외한 line L은 바로 (u,v)의 homogeneous coordinate가 됨.
(추가된 element를 scaling factor라고 부르며, 0인 경우엔 point가 아닌 vector 를 의미함)
origin을 카메라의 초점으로 생각하면 해당 line상의 모든 점이 image plane의 하나의 점에 투영됨
2. Homogeneous Coordinates (동차 좌표)에서의 Point (점)와 Vector (벡터)의 구분
2-1. Point (점)
일반적인 Point (점)은 Homogeneous Coordinates (동차 좌표)로 (x,y,w) 형태로 표현되며, 여기서 w≠0임.
- 예를 들어, Euclidean Plane (유클리드 평면)의 Point (점) (2,3) 는 Homogeneous Coordinates (동차 좌표)로 (2,3,1)로 표현될 수 있음.
- 다른 예로, Point (점) (4,5) 는 Homogeneous Coordinates (동차 좌표)로 (4,5,1), (8,10,2), (12,15,3) 등으로 표현될 수 있음.
- w≠0 인 경우, 이를 Euclidean Coordinates (유클리드 좌표)로 변환할 때 (x/w,y/w)로 변환됨.
2-2. Vector (벡터)
Vector (벡터)는 방향과 크기를 나타내며, Homogeneous Coordinates (동차 좌표)로 (x,y,0) 형태로 표현됨.
- Vector (벡터)는 시작점이 없으며 순수한 방향과 크기만을 나타냄.
- 예를 들어, Vector (벡터) (2,3) 는 Homogeneous Coordinates (동차 좌표)로 (2,3,0)로 표현됨.
- 다른 예로, Vector (벡터) (1,2) 는 Homogeneous Coordinates (동차 좌표)로 (1,2,0)로 표현됨.
Euclidean Geometry (유클리드 기하학)에서는 좌표 (2,3)만으로는 Point (점)인지 Vector (벡터)인지 구분할 수 없으나, 문맥에 따라 구분됨.
- Point (점)은 공간 내의 특정 위치를 나타내는 반면, Vector (벡터)는 시작점과 끝점을 갖지 않고 방향과 크기를 나타냄.
- 예를 들어, Euclidean Geometry (유클리드 기하학)에서 Point (점) (2,3)는 특정 위치를 나타내지만,
- Vector (벡터) (2,3)는 원점에서 시작하여 (2,3) 으로 향하는 방향과 크기를 의미함.
3. Ideal Point (이상점)의 정의
3-1. Ideal Point의 Homogeneous Coordinates
Ideal Point (이상점)은 Homogeneous Coordinates (동차 좌표)에서 w=0 인 점을 의미함.
- 이는 무한히 먼 곳에 위치하는 점으로, 방향을 나타내는 Vector (벡터)의 형태를 취함.
- Ideal Point (이상점)은 (x,y,0)로 표현
- 이는 Vector (벡터)의 Homogeneous Coordinates (동차 좌표) 표현과 동일함.
- 예를 들어, Ideal Point (이상점) (1,2)는 Homogeneous Coordinates (동차 좌표)로 (1,2,0)로 표현됨.
- w=0이기 때문에 Euclidean Coordinates (유클리드 좌표)로 변환할 수 없으며, 이는 Ideal Point (이상점)이 유한한 위치에 있지 않음을 의미함.
3-2. 평행선의 교차
Euclidean Geometry (유클리드 기하학)에서 평행선은 서로 교차하지 않지만,
Projective Geometry (사영 기하학)에서는 무한히 먼 곳에서 교차한다고 간주함.
이 교차점이 바로 Ideal Point (이상점)임.
- 예를 들어, 평행한 두 선 y=2x+1과 y=2x+3은 동일한 기울기 2를 가짐.
- 이 평행선들은 Homogeneous Coordinates (동차 좌표)에서 (2,−1,0)이라는 동일한 Ideal Point (이상점)에서 교차함.
3-3. Vector와 Ideal Point의 관계
Vector (벡터)는 특정 방향을 나타내며, Ideal Point (이상점) 역시 해당 방향으로 무한히 먼 곳에 있는 점을 의미함.
- 예를 들어, Vector (벡터) (3,4)는 Homogeneous Coordinates (동차 좌표)로 (3,4,0)로 표현되며,
- 이는 해당 방향의 Ideal Point (이상점)을 나타냄.
4. Homogeneous Coordinates (동차 좌표)에서의 Line (직선)의 표현
4-1. Line의 Homogeneous Coordinates 표현
Homogeneous Coordinates (동차 좌표)에서는 2D 평면의 직선이 세 개의 동차 좌표 [a,b,c]로 표현됨.
이는 다음과 같은 방정식을 만족함:
ax+by+cw=0
- 여기서 w 는 Homogeneous Coordinates (동차 좌표)의 세 번째 좌표임.
- w가 0이 아닌 경우, 이는 유한한 위치에 있는 직선을 나타내며,
- w가 0인 경우, 이는 Line at Infinity (무한 원선)과 관련된 직선을 나타냄.
4-2. 두 점을 잇는 직선 구하기
두 점 p1=(x1,y1,w1) 과 p2=(x2,y2,w2) 를 잇는 직선을 구하기 위해, 두 점의 cross product (외적)을 계산함:
l=p1×p2
이 cross product (외적)의 결과로 얻어진 벡터 l=(a,b,c)는 두 점을 통과하는 직선의 방정식을 제공함:
ax+by+cw=0
2024.06.28 - [.../Linear Algebra] - [LA] Matrix Multiplication for Cross Product
[LA] Matrix Multiplication for Cross Product
특정 vector와의 cross product를 matric multiplication의 형태로 표현하기도 한다. 벡터 a와 b의 Cross Product(교차곱 or 벡터곱) a×x는 다음과 같이 나타낼 수 있음:$$\mathbf{
dsaint31.tistory.com
4-3. 두 직선의 교점 구하기
두 직선 l1=(a1,b1,c1)과 l2=(a2,b2,c2)의 교점을 구하기 위해, 두 직선의 cross product (외적)을 계산함:
p=l1×l2
- 이 cross product (외적)의 결과로 얻어진 벡터 p=(x,y,w)는 두 직선의 교점의 Homogeneous Coordinates (동차 좌표)를 제공함.
- 여기서 w≠0이면 유한한 점에서 교차하고, w=0이면 Line at Infinity (무한 원선)에서 교차함을 의미함.
5. Line at Infinity (무한 원선)의 의미
5-1. Line at Infinity의 정의
Homogeneous Coordinates (동차 좌표) 시스템에서
l=[0,0,1]⊤는 Line at Infinity (무한 원선)을 나타냄.
- 이는 Projective Geometry (사영 기하학)에서 중요한 개념으로,
- Euclidean Geometry (유클리드 기하학)에서는 무한히 멀리 떨어진 평행선들이 만나는 선을 의미함.
5-2. Line at Infinity의 특성
Line at Infinity (무한 원선)은 모든 Ideal Point (이상점)을 포함하는 직선임.
- 이는 평면 위의 모든 직선이 무한히 멀리서 만나는 지점을 나타냄.
- Homogeneous Coordinates (동차 좌표) 시스템에서, 이 Line at Infinity (무한 원선)은 [0,0,1]⊤로 표현됨.
- 즉, 이 직선은 w가 0인 모든 점들을 포함함.
5-3. Line at Infinity의 표현 비교
Homogeneous Coordinates (동차 좌표)에서 Line at Infinity (무한 원선)을 [0,0,1]⊤로 표현하는 경우와 [0,0,2]⊤로 표현하는 경우는 본질적으로 동일함.
- 이는 Homogeneous Coordinates (동차 좌표)에서 스케일링 인자 w 는 비례적으로 동일한 선을 나타내기 때문임.
- 따라서 [0,0,1]⊤ 와 [0,0,2]⊤는 동일한 Line at Infinity (무한 원선)을 의미함.
5-4. Ideal Points와 Line at Infinity
Line at Infinity (무한 원선)은 모든 Ideal Points (이상점)을 포함함.
각 Ideal Point (이상점)은 다음과 같이 표현될 수 있음:
p=(x,y,0)
Ideal Points (이상점)들이 연결되는 Line at Infinity (무한 원선)은 다음과 같은 일반 형태를 가짐:
0x+0y+1w=0
- 이는 Line at Infinity (무한 원선)의 방정식임.
- 여기서 w=0인 모든 점들은 이 방정식을 만족하며, 따라서 Ideal Points (이상점)들이 모두 이 직선 위에 놓이게 됨.
6. 요약
6-1. Ideal Point의 요약
- Ideal Point (이상점)은 Homogeneous Coordinates (동차 좌표) 시스템에서 Vector (벡터)의 형태 (w=0)를 취하는 점임.
- 이는 무한히 먼 곳에 위치하며, 평행선이 무한히 먼 곳에서 교차하는 점을 나타냄.
- Homogeneous Coordinates (동차 좌표)에서 Point (점)와 Vector (벡터)의 차이를 이해함으로써,
- Ideal Point (이상점)이 유한한 위치의 점이 아닌 방향을 나타내는 무한히 먼 점임을 명확히 알 수 있음.
6-2. Projective Geometry에서 Homogeneous Coordinates의 이점
- Projective Geometry (사영 기하학)에서는 Homogeneous Coordinates (동차 좌표)를 사용하여
- Point (점)와 Vector (벡터)를 명확히 구분할 수 있어, 변환의 일관성과 계산의 정확성을 높이는 이점이 있음.
- 또한, Line at Infinity (무한 원선)의 개념은
- Projective Geometry (사영 기하학)에서 Euclidean Plane (유클리드 평면)의 모든 평행선이 무한히 먼 곳에서 만나는 직선을 표현하며,
- 이는 평면의 모든 직선이 무한히 멀리서 교차하는 지점을 포함함.
같이 보면 좋은 자료들
[CV] Intersection and Ideal Point; Homogeneous Coordinate and Cross Product
Intersection and Ideal Point이 글에서는 homogeneous coordinates(동차 좌표)와 cross product(교차곱)을 이용하여 두 직선의 교점을 찾는 방법을 다룸.또한, 평행한 직선의 경우에 ideal point(이상점)이 나오는 경우
dsaint31.tistory.com
2024.06.16 - [.../Math] - [Math] Geometry: Euclidean, Projective, Non-Euclidean
[Math] Geometry: Euclidean, Projective, Non-Euclidean
Euclidean Geometry(유클리드 기하학), Projective Geometry(사영 기하학), Non-Euclidean Geometry(비유클리드 기하학)기하학(Geometry)은 공간과 도형의 성질을 연구하는 수학의 한 분야임.기하학은 여러 종류가 있
dsaint31.tistory.com
2024.06.13 - [분류 전체보기] - [CV] Homography 에 대해서
[CV] Homography 에 대해서
Homographic transformation 이란Homographic transformation(호모그래피 변환)은projective transformation(투영 변환) 또는homography(호모그래피)라고도 불리며,한 평면의 점들을 다른 평면의 점들로 매핑하는 기하학적
dsaint31.tistory.com
'... > Math' 카테고리의 다른 글
| [Math] Example of Lagrange Method (0) | 2024.06.19 |
|---|---|
| [Math] Geometry: Euclidean, Projective, Non-Euclidean (0) | 2024.06.16 |
| [CV] Intersection and Ideal Point; Homogeneous Coordinate and Cross Product (1) | 2024.06.16 |
| [Math] Weighted Least Square (1) | 2024.06.13 |
| [ML] Bootstrap Sampling (2) | 2024.06.05 |