[CV] Intersection and Ideal Point; Homogeneous Coordinate and Cross Product

Intersection and Ideal Point

이 글에서는 homogeneous coordinates(동차 좌표)와 cross product(교차곱)을 이용하여 두 직선의 교점을 찾는 방법을 다룸.

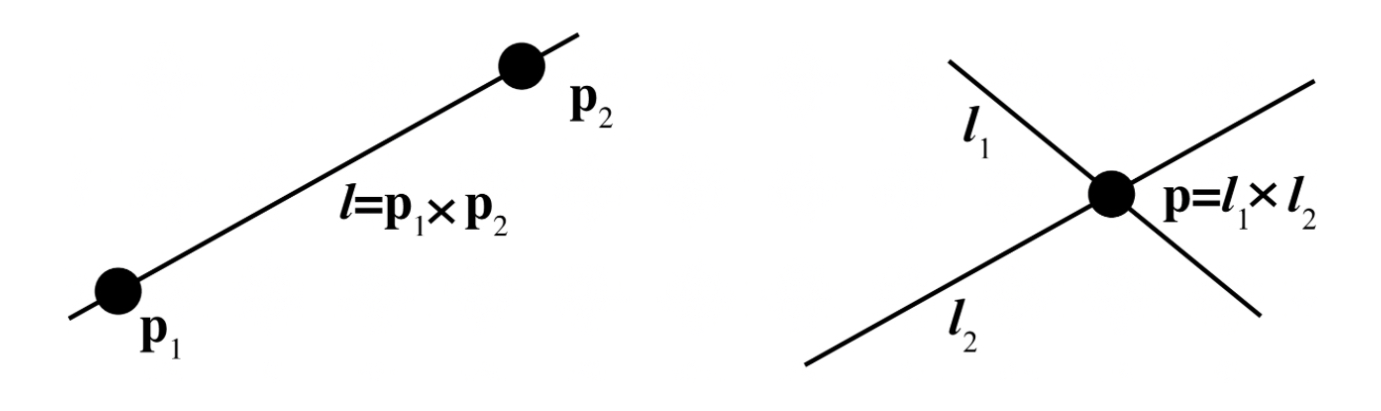
또한, 평행한 직선의 경우에 ideal point(이상점)이 나오는 경우도 다룸.

---

두 직선의 교점을 구하는 방법

단계별 설명

1. Homogeneous Coordinates(동차 좌표):

주어진 두 직선을 동차 좌표 $\mathbf{l}_1 = \begin{bmatrix}a_1 & b_1 & c_1\end{bmatrix}^\top$와 $\mathbf{l}_2 = \begin{bmatrix} a_2& b_2 & c_2\end{bmatrix}^\top$로 표현함.

---

2. Cross Product Calculation(교차곱 계산):

두 직선의 cross product 계산하여 교점 $\mathbf{p} = \mathbf{l}_1 \times \mathbf{l}_2$을 구함.
이는 다음과 같이 계산됨:
$$\mathbf{p} = \mathbf{l}_1 \times \mathbf{l}_2 = \begin{vmatrix}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
a_1 & b_1 & c_1 \\
a_2 & b_2 & c_2
\end{vmatrix}$$

 

계산 결과는 $\mathbf{p} = (b_1c_2 - b_2c_1)\mathbf{i}+ (c_1a_2 - c_2a_1)\mathbf{j} + (a_1b_2 - a_2b_1)\mathbf{k}$임.

---

3. Conversion to Cartesian Coordinates(데카르트 좌표계로 변환):

동차 좌표 $\mathbf{p} = (x_h, y_h, w_h)$를 데카르트 좌표계로 변환하여 교점을 얻음.
이는 다음과 같이 변환됨:
$$(x, y) = \left( \frac{x_h}{w_h}, \frac{y_h}{w_h} \right)$$

---

예제

주어진 두 직선의 동차 좌표가 다음과 같다고 가정함:

$$\mathbf{l}_1 = (1, -1, 2)^\top \\
\mathbf{l}_2 = (2, 1, -3)^\top$$

 

이제, 두 직선의 cross product(or vector product)을 계산함:

$$\mathbf{p} = \mathbf{l}_1 \times \mathbf{l}_2 = \begin{vmatrix}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
1 & -1 & 2 \\
2 & 1 & -3
\end{vmatrix}$$

 

위의 determinant(행렬식)을 계산하면:

$$\mathbf{p} = ( (-1) \cdot (-3) - 2 \cdot 1) \mathbf{i}+ (2 \cdot 2 - (-3) \cdot 1)\mathbf{j}+ (1 \cdot 1 - (-1) \cdot 2 )\mathbf{k}$$

 

단순화하면:

$$\mathbf{p} = (3 - 2, 4 + 3, 1 + 2) \\
\mathbf{p} = (1, 7, 3)$$

 

이제, 동차 좌표 $\mathbf{p} = ( 1, 7, 3 )$를 데카르트 좌표계로 변환함:

$$(x, y) = \left( \frac{1}{3}, \frac{7}{3} \right)$$

 

따라서, 직선 $\mathbf{l}_1 = \begin{bmatrix}1& -1& 2\end{bmatrix}^\top과 \mathbf{l}_2 = \begin{bmatrix}2 & 1 & -3\end{bmatrix}^\top$의 교점은:

$$\left( \frac{1}{3}, \frac{7}{3} \right)$$

 

이 예제는 동차 좌표계에서 교차곱(cross product)을 사용하여 두 직선의 교점을 구하고 이를 데카르트 좌표계로 변환하는 방법을 보여줌.

---

평행한 경우 (Parallel Lines)

두 직선이 평행한 경우에도 cross product 통해 교점을 구할 수 있음.

 

하지만 평행한 경우 교차곱의 결과가 ideal point(이상점)을 나타냄.

ideal pointg은 동차 좌표계에서 $(x_h, y_h, 0)$ 형태로 나타나며, 이는 직선이 교차하지 않는 경우를 의미함.

 

예를 들어, 두 평행한 직선 $\mathbf{l}_3 = (1, -1, 2)^\top$과 $\mathbf{l}_4 = (1, -1, -1)^\top$를 고려하면:

$$\mathbf{p} = \mathbf{l}_3 \times \mathbf{l}_4 = \begin{vmatrix}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
1 & -1 & 2 \\
1 & -1 & -1
\end{vmatrix}$$

 

계산하면:

$$\mathbf{p} = ( (-1) \cdot (-1) - 2 \cdot (-1))\mathbf{i}+ (2 \cdot 1 - (-1) \cdot 1)\mathbf{j}+ (1 \cdot (-1) - (-1) \cdot 1 )\mathbf{k} $$

 

단순화하면:

$$\mathbf{p} = (1 + 2, 2 + 1, -1 + 1)$$
$$ \mathbf{p} = (3, 3, 0)$$

이 결과는 ideal point(이상점)을 나타내며, 이는 두 직선이 Euclidean Geometry에서는 평행하여 교차하지 않음을 의미함.

---

같이 보면 좋은 자료

2024.06.16 - [.../Math] - [Math] Projective Geometry에서 Homogeneous Coordinate로 본 point, vector and line.

[Math] Projective Geometry에서 Homogeneous Coordinate로 본 point, vector and line.

 

---