[SS] Energy Signal vs. Power Signal

https://electronicsprojects.in/signals_and_systems/energy-and-power-signal-difference-diagram-and-information/

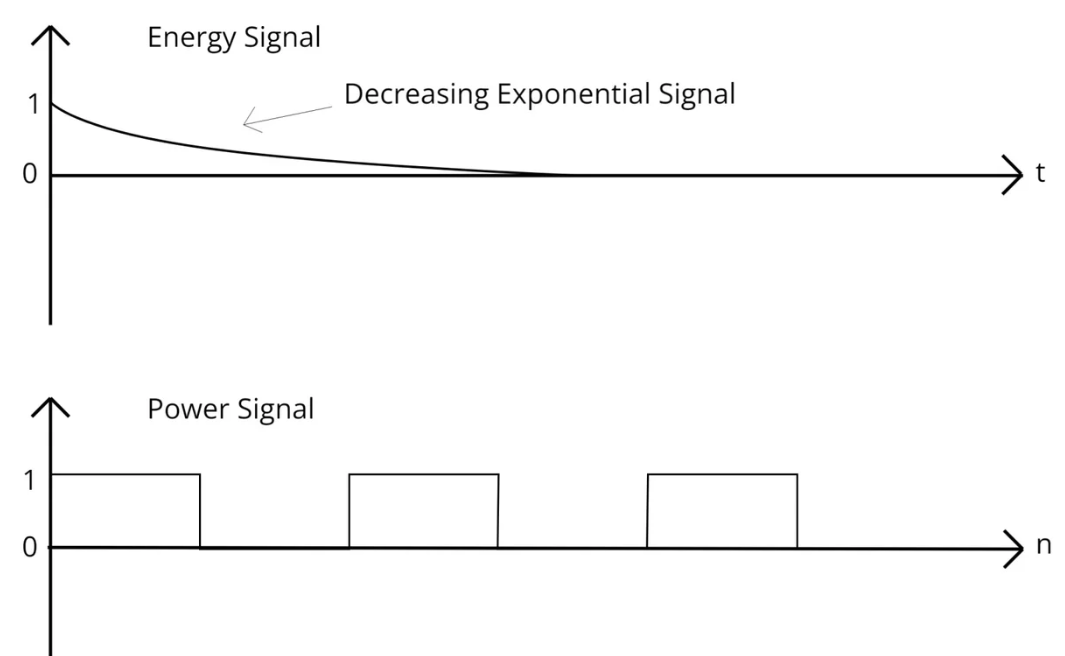
Energy Signal

• Energy 가 유한한 Signal
• Power는 0임.

continuous signal $x(t)$가 Energy signal인 경우, 다음이 성립

$$
E= \underset{T\to \infty}{\lim}\displaystyle \int^{\frac{T}{2}}_{-\frac{T}{2}} |x(t)|^2 dt < \infty
$$

discrete signal $x[n]$이 Energy signal인 경우, 다음이 성립

$$
E= \underset{N\to \infty}{\lim}\displaystyle \sum^{N}_{n=-N} |x[n]|^2 < \infty
$$

finite duration signal이나 exponetial decay signal들이 대표적인 energy signal임.

---

Power Signal

• Energy는 무한하지만, Power가 유한 한 signal.

continuous signal $x(t)$가 Energy signal인 경우, 다음이 성립

$$
E= \underset{T\to \infty}{\lim}\displaystyle \frac{1}{T}\int^{\frac{T}{2}}_{-\frac{T}{2}} |x(t)|^2 dt < \infty
$$

discrete signal $x[n]$이 Energy signal인 경우, 다음이 성립

$$
E= \underset{N\to \infty}{\lim}\displaystyle \frac{1}{2N+1}\sum^{N}_{n=-N} |x[n]|^2 < \infty
$$

infinite periodic signal이 대표적인 power signal임.

energy signal와 power signal 둘 다 아닌 signal도 많음 :
대표적인 예가 ramp signal임.

 

2023.07.05 - [.../Signals and Systems] - [SS] Ramp Function

[SS] Ramp Function

---

참고자료

2023.06.16 - [.../Signals and Systems] - [SS] Signal의 정량적 특성

[SS] Signal의 정량적 특성

---