Shifting
Signal을 지연(delay) 또는 선행(advanced)시키는 연산을 의미함 (보통 delay를 기준으로 처리)
$$x(t) \rightarrow x(t-t_0)$$
- 위 식은 $t_0$로 shift 시킨 것을 의미함. (delayed)
다음 그림은 $x(t)=t^2$ signal과 이를 1, 2로 shift 시킨 signal을 waveform으로 나타낸 것임.

Reflecting
반사라고도 애기를 하며, time signal의 경우 대부분 horizontal reflection을 의미함.
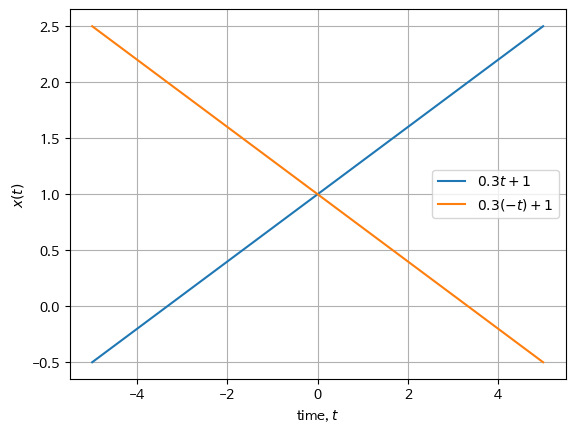
$$x(t) \rightarrow x(-t)$$
- 위 식은 $x(t)$로 reflection 시킨 것을 의미함.
다음 그림은 $x(t)=0.3t+1$ signal과 이를 reflection shift 시킨 signal을 waveform으로 나타낸 것임.
(Time) Scaling
expansion, contraction이라고도 불리며 수식으로 나타내면 다음과 같음.
$$x(t) \rightarrow x(at)$$
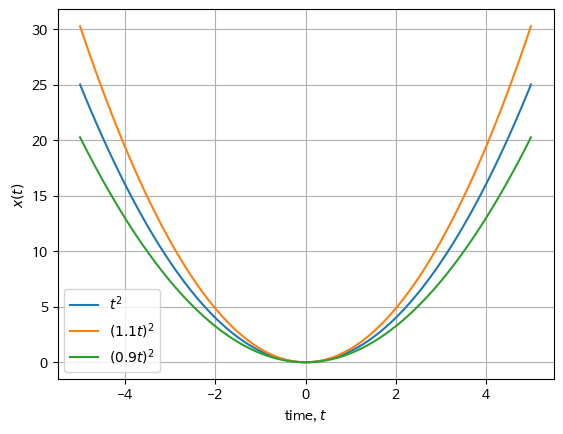
- $a$는 scaling factor임. 1보다 작을 경우 expansion, 1보다 클 경우 contractino임.
다음 그림은 $x(t)=t^2$ signal과 이를 $a=1.1$과 $a=0.9$로 scaling 시킨 signal을 waveform으로 나타낸 것임.
Not Commutative
주의할 것은 shifting, relrecting, scaling 들은 commutative 하지 않음. <= 교환법칙이 성립하지 않음.
다음 예를 보자.
$$x(2t-10)=x(2(t-5))\ne x(2t-5)$$
위 식에서 알 수 있듯이
- 2로 scaling 후 5만큼 shifting한 signal(맨 오른쪽 식)과
- 5로 shifting을 먼저 하고 2로 scaling을 한 signal (중간식)은 다르다.
참고자료
https://gist.github.com/dsaint31x/6d54106c58d70e5db1e0320897f4abc8
SS_shifting_reflecting_scaling.ipynb
SS_shifting_reflecting_scaling.ipynb. GitHub Gist: instantly share code, notes, and snippets.
gist.github.com
'... > Signals and Systems' 카테고리의 다른 글
| [SS] Pulse Signal : Rect function (0) | 2023.07.05 |
|---|---|
| [SS] Unit Step Function (Heaviside Step Function) (0) | 2023.07.05 |
| [SS] Continuous Signals vs. Discrete Signals (0) | 2023.07.05 |
| [SS] Energy Signal vs. Power Signal (1) | 2023.06.19 |
| [SS] Deterministic signal vs. Random signal (0) | 2023.06.19 |