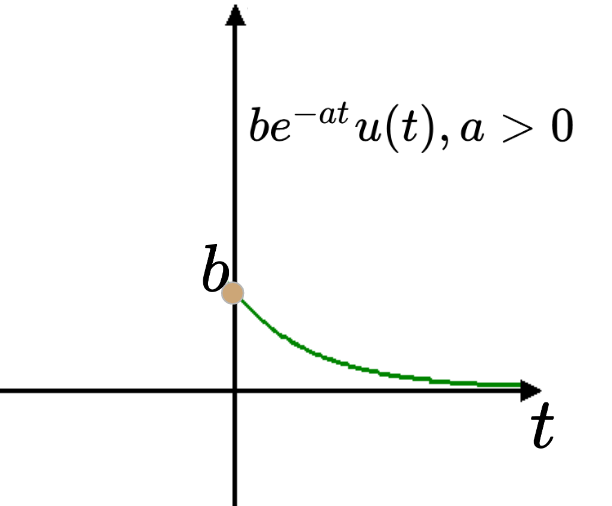
[SS] Fourier Transform of Real Exponential Function
·
.../Signals and Systems
다음과 같은 Real Exponential Function이 있다고 하자. $$b e^{-at} u(t), a>0$$ 해당 Real Exponential Function의 Fourier Transform은 다음과 같음. $$\begin {align} \int^\infty_{-\infty}b e^{-at} u(t)e^{-j\Omega t} \text{d}t &= b \int^{\infty}_{-\infty}u(t)e ^{-(a+j\Omega)t}\text{d}t\\ \quad &= b \int^{\infty}_{0}e ^{-(a+j\Omega)t}\text{d}t\\ \quad &= b \left [ \frac{e ^{-(a+j\Omega)t}}{-(a+j\Omega)}\right]^\infty_0\\ \..


