[SS] Differential Equation and Response (zero-input, zero-state, natural, forced) w/ Laplace Transform
·
.../Signals and Systems
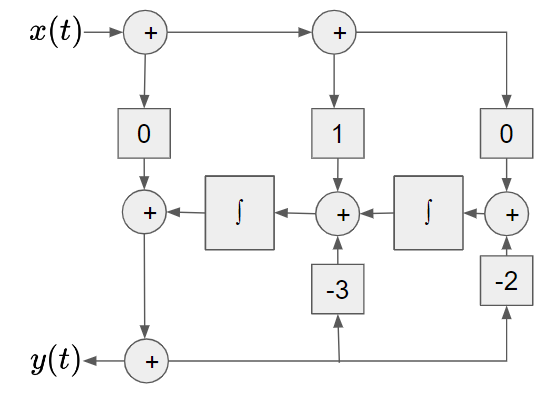
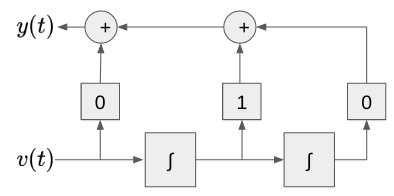
Laplace Transform을 이용한 Differential Equation을 풀기. 문제 다음 미분방정식 의 시스템이 있다고 하자. $$ \frac{d^2 y(t)}{dt^2} + 3\frac{dy(t)}{dt}+2y(t)=\frac{dx(t)}{dt} $$ 아래와 같은 입력과 초기조건에서 zero-state response (초기조건이 0.) zero-input response (input이 0.) natural response (system mode만으로 구성.) forced response (input signal에만 의한 항으로 구성.) 를 구하라. input signal $$ x(t)=t^2+5t $$ initial conditions $$ y(0^-)=2 \\ \frac{dy(0^-)}{..