Activation

[Math] Derivative of Logistic Function

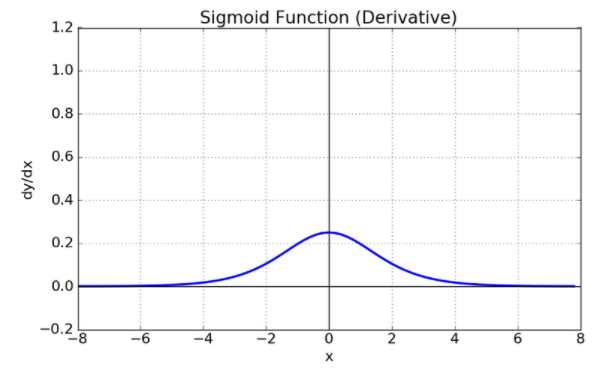
Derivative (도함수) of Logistic Function (Sigmoid라고도 불림) $y=\sigma(x)=\dfrac{1}{1+e^{-x}}$ 를 미분하면 다음과 같음. $$\frac{d}{dx}\sigma(x)= \sigma(x)(1-\sigma(x))$$ graph 유도 유도는 다음과 같음. $$\begin{aligned}\frac{d}{dx}\sigma(x)&= \dfrac{0\times(1+e^{-1}) - 1\times(-e^{-1})}{(1+e^{-x})^2}\\&=\dfrac{e^{-x}}{(1+e^{-x})^2}\\ &= \frac{1}{(1+e^{-x})}\frac{e^{-x}}{(1+e^{-x})}\\ &= \frac{1}{(1+e^{-x})}\left( 1-\dfrac{..

[DL] Softsign : tanh의 유사품

hyperbolic tangent (=tanh)와 유사한 함수. tanh 대신 activation function으로 사용되는 경우도 있음. $$\text{softsign}(x)=\frac{x}{1+|x|}$$ softsign의 derivative는 다음과 같음. $$\dfrac{d}{dx}\text{softsign}(x)=\dfrac{1}{\left(1+|x|\right)^2}$$ 차트 비교 관련소스 import numpy as np import matplotlib.pyplot as plt x = np.linspace(-20.,20., 100) softsign = x/ (1.+np.abs(x)) logistic = 1/ (1+np.exp(-x)) tanh = np.tanh(x) fig,ax = plt...

[DL] Hyperbolic Tangent Function (tanh)

logistic function과 함께 sigmoid의 대표적인 함수가 바로 $\text{tanh}$임. 값이 $[-1,1]$의 range를 가지며, logistic에 비해 기울기가 보다 급격하기 때문에 좀 더 빠른 수렴속도를 보임. 하지만, sigmoid의 일종이기 때문에 gradient vanishing에 자유롭지 못함. logistic보단 그래도 양호. 양 끝단에 갈 경우, 거의 기울기가 0임 RNN의 activation function으로 많이 이용된다. Exploding gradient가 쉽게 발생하는 RNN에서는 ReLU가 적합하지 않음. ReLU는 positive영역에서 기울기가 1로 계속해서 고정되면서, 결과값이 항상 0이상의 값으로 나오기 때문에 , 지나치게 gradient가 커지는 ex..

[Math] Sigmoid function

S자형 곡선을 갖는 함수. (대표적인 예가 logistic function이나 sigmoid는 다음과 같이 여러 종류가 있음) Artificial Neural Network의 Artificial Neron의 Activation function으로 초창기에 많이 사용되었음. Logistic distribution, normal distribution, student $t$ distribution등의 probability distribution(확률 분포)들의 cumulative distribution function (cdf)이 바로 sigmoid function임. 때문에 sigmoid function에 대한 derivative는 normal distribution처럼 대칭이고 종모양의 분포를 보이는 함..

[ML] Logit에서 Logistic Function.

Logistic FunctionLogistic function은일종의 연속변수에 해당하는 "raw score"(정확히는 logit score)을 probability로 바꾸어주는 함수임: output이 0에서 1사이의 real number.미분가능!더보기Binary classification에서 True일 경우의 logit score가 0이상일 경우, True일 확률이 0.5이상에 해당한다.즉,  logit score 의 값이 양수로 클수록 대응하는 확률이 0.5보다 커지며, 음수로 커질수록 대응하는 확률이 0.5 이하록 작아짐.다음이 바로 logistic function임. $$\text{logistic}(t)=\sigma(t)=\frac{1}{1+e^{-t}}$$Sigmoid functions 중에서..

Softplus

다음과 같은 함수를 softplus라고 하며, ANN에서 activation function으로 사용됨. $$\begin{aligned}\zeta(x)&=\log(1+e^x)\\&=\log(1+e^{-|x|})+\max(0,x)\end{aligned}$$ exponential function과 Logarithmic function을 더한 함수 (즉, Transcendental function의 하나임). y=max(x,0)(ReLU)와 매우 비슷하나 $x=0$ 근처에서 값이 보다 부드럽게 변함 (미분 가능) 위 식에서 $\log(1+e^x)$는 정의이고, 실제 ML등에서 사용되는 건 $\log(1+e^{-|x|})+\max(0,x)$ 임. $x$가 100정도만 되어도 정의식의 경우 numerical is..