[DL] Hyperbolic Tangent Function (tanh)

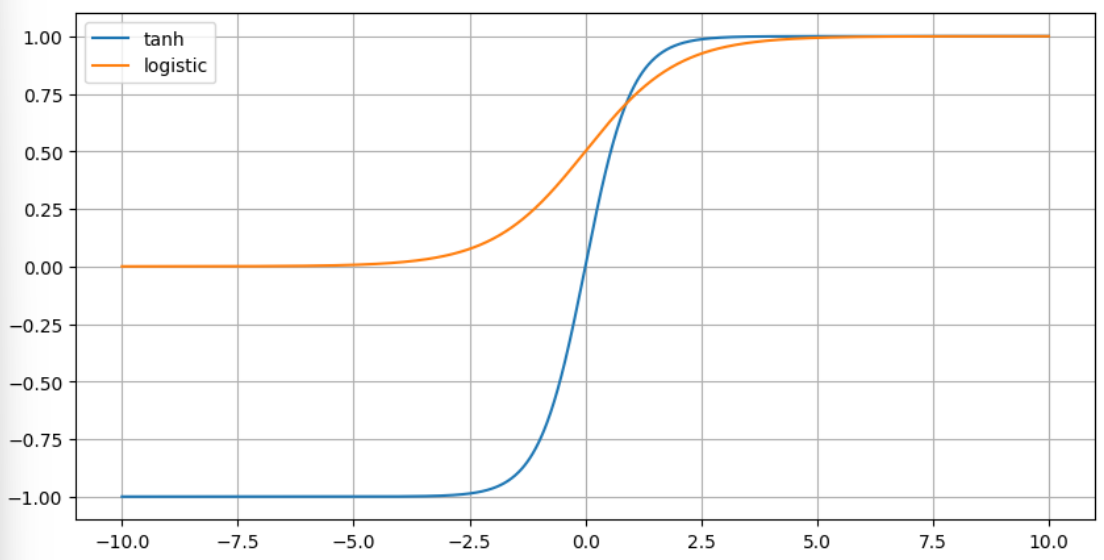
logistic function과 함께 sigmoid의 대표적인 함수가 바로 $\text{tanh}$임.

• 값이 $[-1,1]$의 range를 가지며, logistic에 비해 기울기가 보다 급격하기 때문에 좀 더 빠른 수렴속도를 보임.
• 하지만, sigmoid의 일종이기 때문에 gradient vanishing 에 자유롭지 못함.
  • logistic보단 그래도 양호한 편이나
  • sigmoid의 일종이기 때문에, 양 끝단에 갈 경우 기울기가 0에 수렴.
• RNN의 activation function으로 많이 이용된다.
  • Exploding gradient가 쉽게 발생하는 RNN(Recurrent Neural Network)에서는 ReLU가 적합하지 않음.
    • Weight matrix의 eigenvalue (특히, max eigenvalue)가 1보다 클 경우, time series의 길이만큼 여러번 해당 eigenvalue가 곱해지는 형태로 출력이 결정됨.
    • 이는 gradient 를 매우 심하게 커지게 하여 exploding gradient를 일으킴 
    • 물론 eigenvalue가 1보다 작으면 이는 vanishing gradient로 이어짐.
    • RNN이 모든 Time Step에서 동일한 가중치 행렬을 공유하기 때문에 이에 대한 고려가 필요함:
      • 각 layer의 weight matrix가 한 iteration에서 한 번만 영향을 주는 CNN등과의 차이점
      • RNN 이 보다  exploding gradient에 쉽게 발행하는 이유임.
  • ReLU는 positive영역에서 기울기가 1로 계속해서 고정되면서, 결과값이 항상 0이상의 값으로 나오기 때문에 ,
    지나치게 gradient가 커지는 exploding gradient에 자유롭지 못함
    (ReLU는 Gradient Vanishing Problem에 강함).
  • 때문에 아직까지도 RNN에서는 intermediate layers의 activation function으로 사용됨
    (단, RNN이 Transformer로 대체되고 있음. Transformer는 ReLU의 변형인 GeLU를 사용).

정의

Hyperbolic tangent의 정의는 다음과 같음.

$$\text{tanh}(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}=2\sigma(2x)-1$$

• $\sigma(x)=\frac{1}{1+e^{-x}}$ : logistic function.

2022.06.06 - [Computer] - [ML] Logit에서 Logistic Function.

[ML] Logit에서 Logistic Function.

---

---

Differentiation

hyperbolic tangent도 결국 $e^x$에 기반한 형태이기 때문에 derivative가 원래 형태를 기반으로 만들어짐.

logistic function $\sigma(x)$를 기반으로 $\text{tanh(x)}$의 derivative를 유도하면 다음과 같음.

 

$$\begin{aligned}\dfrac{d }{dx}\text{tanh}(x) &= \dfrac{d }{dx}(2\sigma(2x)-1) \\ &= 2 \dfrac{d\sigma(2x)}{dx} \\ &= 2 \sigma(2x) (1-\sigma(2x))\dfrac{d}{dx}(2x) \\ &= 4 \sigma(2x) (1-\sigma(2x)) \\ &= \dfrac{4}{(1+e^{-2x})}\left(1-\dfrac{1}{1+e^{-2x}}\right) \\ &= \dfrac{ 4(1+e^{-2x})-4}{(1+e^{-2x})^2} \\ &= \dfrac{4e^{-2x}}{(1+e^{-2x})^2}\\&=\dfrac{4}{(e^{x}+e^{-x})^2} \\ &= \dfrac{ (e^x+e^{-x})^2 - (e^x-e^{-x})^2}{(e^x+e^{-x})^2} \\ &= 1-\dfrac{(e^x-e^{-x})^2}{(e^x+e^{-x})^2} \\ &= 1-\text{tanh}^2(x)\\&=(1-\text{tanh}(x))(1+\text{tanh}(x))\end{aligned}$$

 

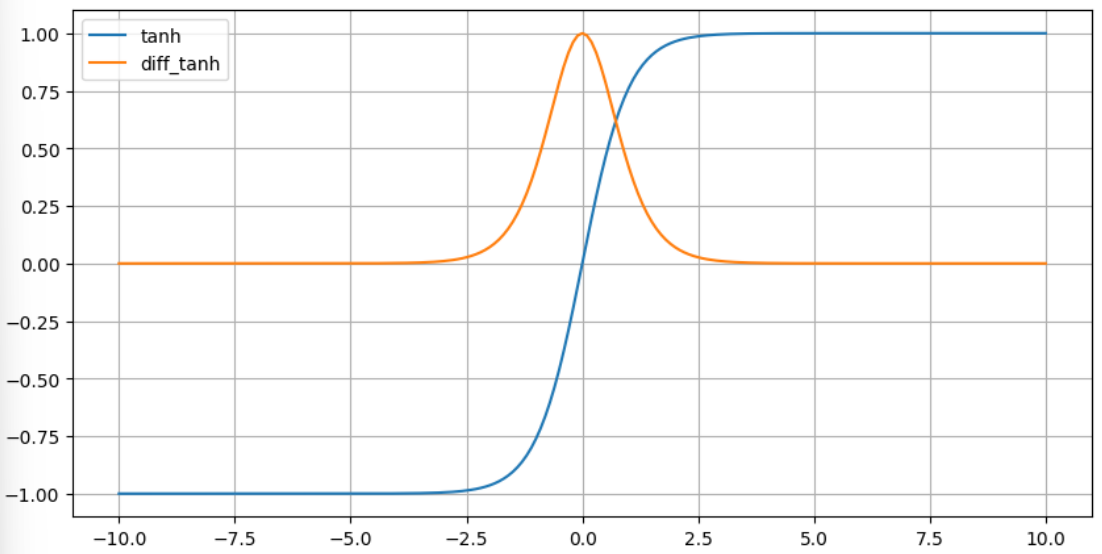
다음은 $\text{tanh}(x)$와 derivative를 같이 그린 그림임.

---

DL에서의 Activation Function

• Logistic 보다 훨씬 큰 derivative (최대값이 4배 큼)를 가지기 때문에
  logistic에 비해 gradinet vanishing에 대한 저항력이 보다 큰 편임.
• tanh 는 $[-1,+1]$의 출력범위와 0인 출력평균을 가지기 때문에 logistic function의 bias shift 를 가지고 있지 않음:
  
  • Logistic function 의 경우,
    • 분포가 0을 중심으로 양과 음이 균형을 이룬 입력( $[-\infty, +\infty]$)에 대해서
    • 0.5를 중심으로 하는 양수 영역($[0,1]$)으로 분포가 이동함 : bias shift !!
  • 다음 layer의 입력은 0을 중심으로 양수와 음수가 균형 잡힌 값이 아니라, 대부분 양수 쪽으로 치우친 값이 되며, 이는 layer를 많이 통과하면서 심해짐.
  • 이는 각 layer의 출력이 sigmoid나 tanh 같은 activation으로 인해 점점 saturation 영역으로 들어갈 가능성이 커짐을 의미.
• 특히 RNN에서는 gradient vanishing뿐만 아니라 gradient exploding 문제도 자주 발생하는데,
  tanh는 양수와 음수 출력을 모두 생성하여 hidden state의 평균을 0 근처로 유지하는 경향이 있어
  Logistic function 보다 안정적인 학습에 유리한 경우가 많음.

 

이같은 이유들로 인해 RNN, LSTM 등에서는 tanh를 activation function으로 사용한다. 

---

더 읽어보면 좋은 자료

2022.12.28 - [.../Math] - [Math] Sigmoid function

[Math] Sigmoid function

https://dsaint31.me/mkdocs_site/ML/ch09/weight_initializations/

BME228

https://dsaint31.tistory.com/581

[DL] Softsign : tanh의 유사품

2024.02.26 - [.../Math] - [Math] Function의 분류: 작성중

[Math] Function의 분류: 작성중

---