728x90
728x90

예제
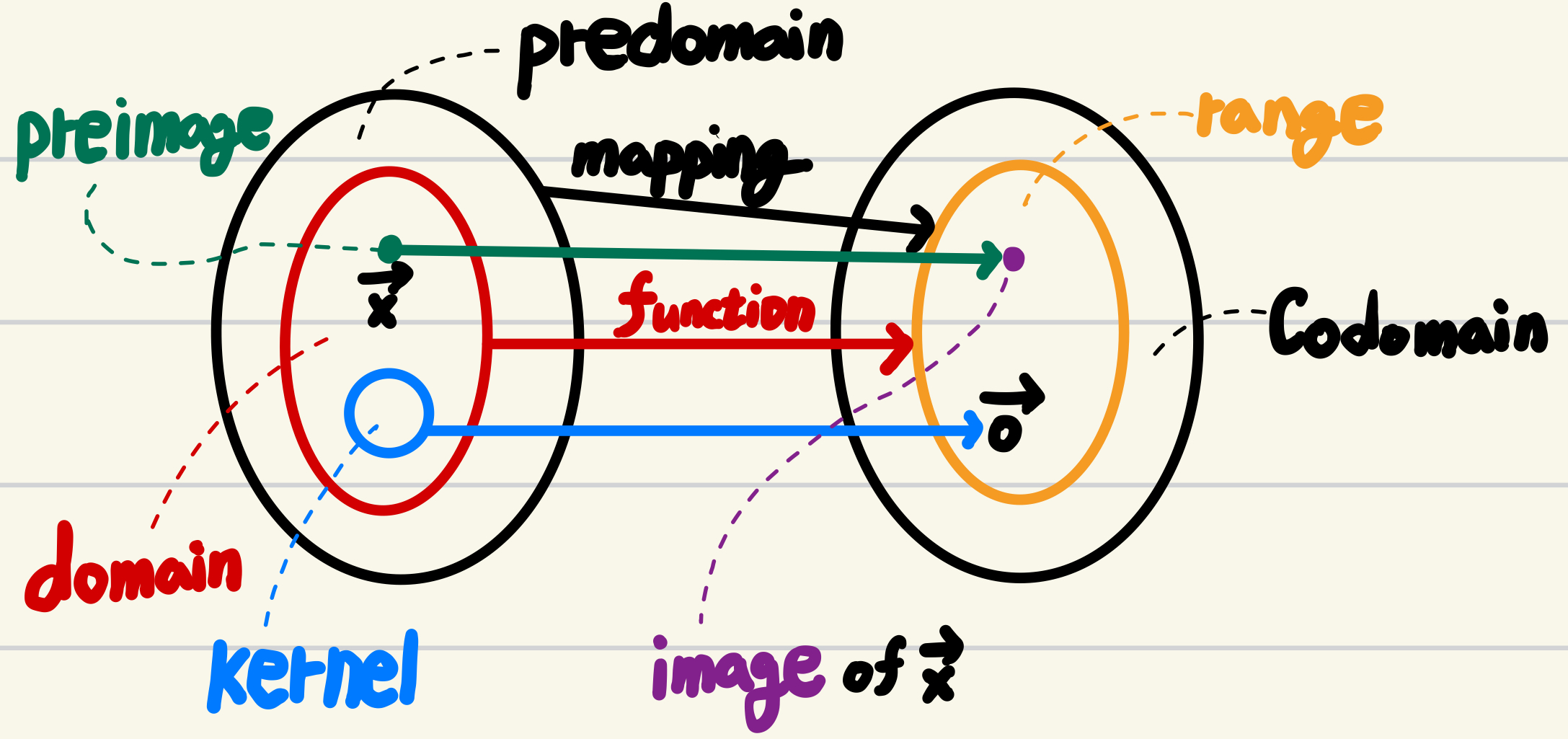
함수 $f(x) = x^2$, domain $X = [-2, 2]$ 를 예제로 하여 domain, codomain, image, range, preimage, coimage 를 구해봄.
Domain (정의역): $X = [-2, 2]$
- 입력값의 범위: $-2 \le x \le 2$
Codomain (공역): $Y = \mathbb{R}$ (실수 전체)
- 가능한 모든 출력값의 집합
Image (상): $\{y | y = x^2, x \in [-2, 2]\}$
- 실제 출력값의 범위
- 최솟값: $x = 0$일 때, $f(0) = 0$
- 최댓값: $x = \pm 2$일 때, $f(\pm 2) = 4$
- 따라서 $\text{image} = [0, 4]$
Range (치역): $[0, 4]$
- image와 동일.
- image들의 집합을 가리키는데 주로 사용되고, 이 경우, image는 range의 한 entry(함숫값 하나)를 가리킴.
Preimage (원상, 역상, Inverse Image):
- codomain의 원소 y에 대한 역상 $f^{-1}(y) = \{x \in X | f(x) = y\}$
- 예시:
- $f^{-1}(0) = \{0\}$
- $f^{-1}(1) = \{-1, 1\}$
- $f^{-1}(2) = \{-\sqrt{2}, \sqrt{2}\}$
- $f^{-1}(4) = \{-2, 2\}$
- $f^{-1}(5) = \emptyset$
- $y \in [0, 4]$일 때만 preimage가 존재
- domain의 subset 에 해당함.
Kernel (커널):
- $\text{ker}(f) = \{x \in X | f(x) = 0\} = \{0\}$
- 함숫값이 0이 되는 모든 $x$값의 집합
Coimage (코이미지, 여상):
- domain $X$의 partition(분할)을 나타내는 Equivalence Class(동치류)들의 집합
- 수학적 표현
- 함수 $f: X \leftarrow Y$에 대해
- $\text{ker}(f) = \{x | f(x)=0\}$ 는 function의 kernel.
- 동치관계: $x_1 \sim x_2 \leftrightarrow f(x_1) = f(x_2)$
- $[x]^f$는 element $x$를 포함하는 Equivalence Class.
- coimage의 특성
- 모든 $x \in X$는 정확히 하나의 Equivalence Class에 속함.
- 같은 동치류에 속한 원소들은 함수 $f$에 의해 같은 값으로 매핑됨.
- coimage는 function의 Kernel 구조를 보여줌
- coimage의 구성:
- Kernel을 하나의 entry로: $[0]^f = \{0\}$
- 나머지 동치류들: $x > 0$에 대해 $[x]^f = \{-x, x\}$
- 예제
- domain $[-2,2]$에서 정의된 함수 $f$가 다음과 같은 성질을 가짐 .
- Kernel은 0 만을 entry로 가짐: $\text{ker}(f) = {0}$ 또는 $[0]^f = {0}$.
- 나머지 Equivalence Class: $x>0$에 대해 $[x]^f = {-x,x}$
- 이 경우 comiage는 다음과 같음.
- $\text{coimage} = \{[0]^f\} \cup \{[x]^f | x \in (0,2]\}$
- 이는 다음과 같은 애기임:
- $\{ [0]^f, [x]^f | x \in (0,2] \} = \{ {0} , \{-x, x\} | x \in (0,2] \}$
- 해석:
- Element $0$는 혼자 하나의 동치류 형성.
- 구간 $(0,2]$의 각 양수 $x$에 대해, $x$와 $-x$가 같은 동치류 형성.
- function $f$는 $x$와 $-x$에 대해 같은 값을 가짐 (원점 대칭 함수)
- domain $[-2,2]$에서 정의된 함수 $f$가 다음과 같은 성질을 가짐 .
Notification:
- Image와 coimage는 canonical isomorphism (동형)관계
- coimage의 각 동치류 $[x]^f$는 image의 한 점 $f(x)$와 일대일 대응
- Domain의 분할 구조:
- 각 $x \in X$는 정확히 하나의 Equivalence class(동치류)에 속함
- 동치류들은 서로 겹치지 않음
- 모든 동치류의 합집합이 domain $X$
- Preimage의 특성:
- $y \in [0, 4]$일 때만 존재
- $y = 0$일 때를 제외하고 모든 $y$값에 대해 두 개의 $x$값을 가짐
- Kernel과 coimage의 관계:
- Kernel은 그 자체로 하나의 동치류
- Kernel(여기서는 $\{0\}$)은 coimage에서 단일 entry $[0]^f$로 취급
- 이는 "kernel을 동일시한다"는 것의 의미
- Coimage의 나머지 entry들은 각각 두 개의 원소로 구성 ($\{-x, x\}$)
- Coimage와 preimage의 관계:
- Coimage의 각 동치류는 특정 $y$값에 대한 preimage와 같은 집합
- 하지만 coimage는 이들의 전체 collection을 domain의 분할로 보는 관점.
같이보면 좋은 자료
2021.09.14 - [.../Math] - Function (함수): 간략 정의
Function (함수): 간략 정의
Function은 흔히 mapping(사상), transformation(변환)이라는 용어로 불리기도 함. set으로 정의한다면, domain(정의역: 일종의 set)의 각 element에 대해co-domain(공역: 역시 일종의 set)의 elements 중 오직 하나 로
dsaint31.tistory.com
https://ics.uci.edu/~alspaugh/cls/shr/correspondence.html
Correspondences
A correspondence f between X and Y is a triple (X,Y,Γ) where Γ is a subset of the Cartesian product X×Y. The pre-domain of f is X. The co-domain of f is Y. Γ is the graph of f. (Note that Γ is a binary relation.) The domain of f (written Dom(f))
ics.uci.edu
728x90
'... > Math' 카테고리의 다른 글
| [Math] Hyperbolic Functions (쌍곡선 함수) (0) | 2025.03.20 |
|---|---|
| [Math] Triangular Inequality (삼각부등식) (0) | 2025.02.10 |
| [Math] Laplace Distribution (1) | 2025.01.13 |
| [Math] Extremum Point, Inflection Point, Saddle Point, Convex and Concave. (2) | 2025.01.05 |
| [Math] Binomial Theorem (이항정리) (0) | 2025.01.04 |