[LA] Null Space

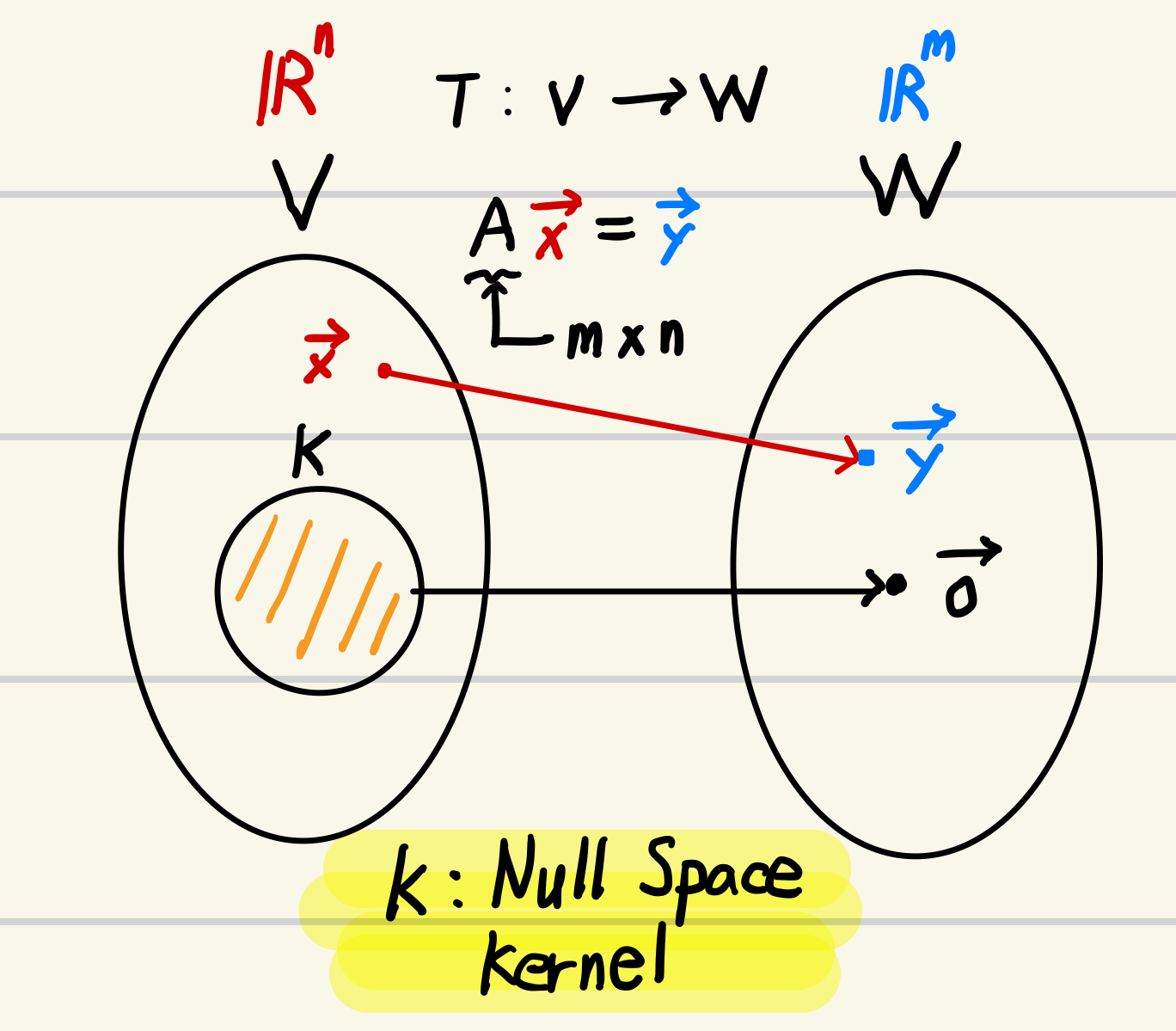
Null Space는 주로 matrix 에 관련된 맥락에서 사용되며,

Linear Transform 의 맥락에서는 Kernel 이라고 불림.

---

Definition : Null Space

The null space of an $m \times n$ matrix $A$, written as Nul$(A)$, is the set of all solutions of the homogeneous equation $A\textbf{x}=\textbf{0}$.

In set notation,

$$\text{Nul }(A) = \left\{ \textbf{x}:\textbf{x} \text{ is in }\mathbb{R}^n \text{ and } A\textbf{x}=\textbf{0} \right\}$$

Kernel and Null space

Null Space 의 차원은 Nullity라고 표현됨:

$$\text{Nullity} = \text{dim}(\text{Nul}(A))$$

---

Theorem 2

The null space of an $m \times n$ matrix $A$ is a subspace of $\mathbb{R}^n$.
Equivalently, the set of all solutions to a system $A\textbf{x}=\textbf{0}$ of $m$ homogeneous linear equations in $n$ unknowns is a subspace of $\mathbb{R}^n$.

 

참고로 subspace는 vector space의 subset이면서 다음의 3가지 조건을 만족하면 됨:

1. zero vector 를 element로 가져야 함.

2. vector addition에 닫혀있어야함.

3. scalar multiplication에 닫혀 있어야 함.

2022.04.05 - [.../Math] - [Math] Definition of Vector Space and Sub-Space

[Math] Definition of Vector Space and Sub-Space

---

Proof

Nul$(A)$ is a subset of $\mathbb{R}^n$ : matrix 의 column 의 수가 $n$임.
because $A$ has $n$ columns.
($\textbf{x}$ is a $n \times 1$ matrix or $n$-entries vector)

 

We need to show that Nul $A$ satisfies the three properties of a subspace.

1. $\textbf{0}$ is in Nul $A$.

---

Next, let $\bf{u}$ and $\bf{v}$ represent any two vectors in Nul$(A)$.

Then

$$A\textbf{u}=\textbf{0} \text{ and } A\textbf{v}=\textbf{0}$$

To show that

2. $\textbf{u} + \textbf{v}$ is in Nul $(A)$,

we must show that $A(\textbf{u}+\textbf{v})=\textbf{0}$.

• Using a property of matrix multiplication, compute

$$A(\textbf{u}+\textbf{v})= A\textbf{u} + A\textbf{v} = \textbf{0}+\textbf{0} = \textbf{0}$$

• Thus $\textbf{u}+\textbf{v}$ is in Nul$(A)$, and Nul$(A)$ is closed under vector addition.

---

Finally, if $c$ is any scalar, then which shows that

3. $c\textbf{u}$ is in Nul$(A)$.

$$A(c\textbf{u}) = c(A\textbf{u}) = c(\textbf{0}) = \textbf{0}$$

---