System of Linear Equations (연립방정식)의 Solution를 구하는 가장 표준적인 방법.
Gauss Elimination을 좀 더 보강한 방법
(컴퓨터 없이 연립일차방정식 계산할 경우 가장 일반적으로 사용됨)
- System의 Augmented Matrix에 Elementary Row Operations을 적용하여 Row Reduction(=행소거, 또는 Elimination으로 볼 수 있음)을 수행.
- Row reduction에 의해 Augmented Matrix는 Row Echelon Form (REF)이 됨. (◀ forward phase종료)
- 이 REF를 backward phase를 수행하여 Reduced Row Echelon Form(RREF)으로 변경하여 solution을 구함.
Pre-Requirement
2024.02.17 - [.../Linear Algebra] - [LA] Row Operations and Row Equivalent
Row Echelon Form (행사다리꼴, REF)
REF는 다음을 만족하는 Matrix로 Augmented Matrix 와 Row Equivalent (=Solution이 변하지 않음).
- 모든 0이 아닌 행은 0으로만 이루어진 행들보다 상단에 위치.
- 각 행의 첫 번째 0이 아닌 원소(pivot위치의 element, leadidng entry)는 그 아래 row의 해당 pivot column보다 왼쪽에 위치 (Upper Triangular Matrix).
- Pivot Column에서 Pivot 보다 아래에 있는 모든 elements는 0.
Pivot은
특정 element 자체를 가리키는 것이 아닌
행과 열의 위치에 해당함.

Pivot and Pivot Column
2024.02.17 - [.../Linear Algebra] - [LA] Pivot and Pivot Column
[LA] Pivot and Pivot Column
Pivot (position) Matrix의 row echelon form(REF)에서 leading entry들의 위치를 가르킴. leading entry : row에서 0이 아닌 첫번째 element를 가르킴. 실제로 REF나 RREF나 pivot position은 같음. RREF는 matrix에 대해 unique하게
dsaint31.tistory.com
Example
다음은 REF의 간단한 예임:
$$\begin{bmatrix}
\blacksquare & * & * & * \\
0 & \blacksquare & * & * \\
0 & 0 & 0 &0
\end{bmatrix}$$
- $\blacksquare$ is a leading entry. (pivot position)
- 1,2 column이 바로 pivot column임.
- $*$: asterisk는 임의의 수를 의미함(0 포함)
REF은
- Augmented Matrix에 Elementary Row Operations을 가해서 만들어지며,
- 가해지는 Elementary Row Operations는 Matrix의 곱을 통해 하나의 Matrix로 표현가능함
- 이는 LU Decomposition에서 Lower Triangular Matrix와 사전에 가해진 Permutation Matrix의 곱에 해당.
Linear System의 Augmented Matrix에 대해
Row Equivalent인 여러 Row Echelon Form (REF)이 존재함: Not Unique
하지만 Reduced Row Echelon Form은 Unique임.
LU Factorization 과 Gauss Elimination
REF는 LU Factorization (or LU Decomposition)과 Gauss Elimination에서 사용됨:
- LU Factorization (with Permutation)에서 Permutation Matrix (=Row Exchange 수행.)와 Lower Triangular Matrix (=연속된 Row Reduction 들 수행의 누적)이 Elementary Row Operations에 대응하고 Upper Triangulation Matrix가 REF에 대응.
- $L$은 대부분 Row Reduction에 대응하는 Elementary Row Opertion Matrix의 곱에 대응.
- LU Factorization의 $L$은 Diagonal이 1이어야 함: Elementary Matrix들은 모두 invertible이므로 이들의 역의 곱인 $L$도 invertible이기 때문임.
- $U$도 엄밀한 Upper Triangulation Matrix (엄밀하게는 Square Matrix)는 아니고, 그와 비슷한 형태(Upper Triangular Form)이라고 봐야함: REF 로서, $A$ 와 Row Equivalent임 (RREF와 달리, pivot의 위치의 요소가 1이 아닐 수 있음)
- Gauss Elimination은 Elementary Row Operations를 각각 대응하는 행렬을 곱(왼쪽에 위치)하는 Linear Transform을 수행하여 Upper Triangular Matrix에 대응하는 REF로로 변환하는 과정을 대수적으로 표현한 것임.
- 결론적으로, LU Factorization은 Gauss Elimination의 또 다른 표현이며, 각각의 행렬이 Elementary Row Operation의 특정 유형에 해당한다고 볼 수 있음.
다음은 LU Factorization을 보여줌:
$$ \begin{aligned} A &= LU \\ A\mathbf{x} &= \mathbf{b} \\ LU\mathbf{x} &=\mathbf{b} \\ L\mathbf{y} &= \mathbf{b} &\quad \text{forward substition} \\ \mathbf{y} &= U \mathbf{x} &\quad \text{backward substittion}\end{aligned}$$
- : 대각선 아래만 값이 있는 Lower Triangular Matrix(하삼각 행렬):
- 주의할 점은 LU Factorization에서 Diagonal 원소는 반드시 1! (Row Reductions에 대응)
- Unit Lower Triangular Matrix임.
- $U$: 대각선 위에만 값(반드시 1일 필요는 없음)이 있는 Upper Triangular Matrix(상삼각 행렬).
- 실제로는 REF임.
그림으로 살펴보면 다음과 같음:
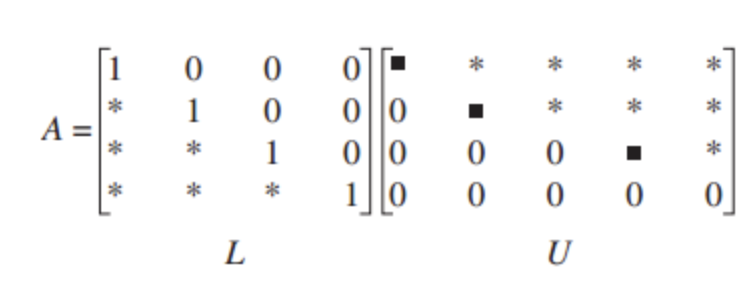
Pivot 위치에 0이 있는 경우엔 Permutation Matrix로 row exchanging을 해주고 LU 분해를 해 줌:
$$PA = LU$$
[LA] 예제: LU Factorization (or LU Decomposition) 와 Gauss Elimination
LU Factorization와 Gauss EliminationLU Factorization은행렬 $A$ 를 다음과 같이 두 행렬 $L$ (Lower Triangular Matrix)와 $U$ (Upper Triangular Matrix)로 분해하는 기법임:$$PA = LU$$여기서 $P$ 는 Permutation Matrix로, 피벗팅(pivoti
dsaint31.tistory.com
https://deep-learning-study.tistory.com/311
[선형대수학] 2.5 LU 분해 - LU decomposition - Factorization, LU 분해 이점, LU 분해 알고리즘
이번 포스팅에서는 LU 분해(LU deposition)에 대해 알아보겠습니다. LU분해는 실제 문제를 해결할때 유용하게 쓰이므로 공대생에게 매우 중요합니다. 1. 분해 - Factorization, decomposition 분해는 하나의 행
deep-learning-study.tistory.com
Reduced Row Echelon Form (기약사다리꼴, RREF)
REF의 조건을 모두 만족하면서 추가 조건이 있음:
- 모든 pivot(각 행의 첫 번째 0이 아닌 element, leading entry)은 1이어야 함.
- 각 pivot은 해당 열에서 유일한 1로, 해당 열의 나머지 원소는 모두 0.
$$\begin{bmatrix}
1 & 0 & * & * \\
0 & 1 & * & * \\
0 & 0 & 0 &0
\end{bmatrix}$$
- REF에서 leading entry 가 1이 되도록 수정됨. (Pivot Position)
- RREF에서 pivot은 해당 column에서 유일하게 0이 아닌 수임.
- REF와 마찬가지로 1,2 column이 바로 Pivot Column임: 각 행에서 1이 최초로 등장하는 열이 Pivot Column임.
REF는 여러 개가 존재하나, RREF는 unique하게 결정됨.
REF가 Gauss Elimination 에 대응한다면, RREF는 Gauss-Jordan Elimination에 대응함.
동시에 LU Decomposition을 조금 개선(?)한 LDU Decomposition에 해당함.
2025.02.05 - [.../Linear Algebra] - [LA] LDU Decomposition (or LDU Factorization)
[LA] LDU Decomposition (or LDU Factorization)
LU factorization 을 조금 변형한 형태. (U가 REF인 LU factorization과 달리, LDU의 경우 RREF임)2024.02.17 - [.../Linear Algebra] - [LA] Gauss-Jordan Elimination (including Gauss Elimination) and LU Factorization [LA] Gauss-Jordan Elimination
dsaint31.tistory.com
Example
아래와 같은 augmented matrix가 있다고 하자. 여기에 Gauss-Jordan Elmination Method를 적용하라.
$$\begin{bmatrix}
0 & 2 & 1 \\
1 & 1 & 2 \\
2 & 1 & 1
\end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix} 4 \\ 6 \\ 7 \end{bmatrix}
\rightarrow
\begin{bmatrix}
0 & 2 & 1 & 4 \\
1 & 1 & 2 & 6 \\
2 & 1 & 1 &7
\end{bmatrix}$$
Solution
1. interchange 수행 ($\text{row}_1$과 $\text{row}_3$를 교체)
$$\begin{bmatrix}
2 & 1 & 1 &7 \\
1 & 1 & 2 & 6 \\
0 & 2 & 1 & 4
\end{bmatrix}$$
2. replacement 수행 ($\text{row}_2= \text{row}_2-\frac{1}{2}\text{row}_1$)
$$\begin{bmatrix}
2 & 1 & 1 &7 \\
0 & 1/2 & 3/2 & 5/2 \\
0 & 2 & 1 & 4
\end{bmatrix}$$
3. 편의를 위해 scaling 수행 ($\text{row}_2= 2\text{row}_2$)
$$\begin{bmatrix}
2 & 1 & 1 &7 \\
0 & 1 & 3 & 5 \\
0 & 2 & 1 & 4
\end{bmatrix}$$
4. replacement 수행 ($\text{row}_3= \text{row}_3 -2\text{row}_2$)
$$\begin{bmatrix}
2 & 1 & 1 &7 \\
0 & 1 & 3 & 5 \\
0 & 0 & -5 & -6
\end{bmatrix}$$
5. backworad pahse 시작 : replacement 수행 ($\text{row}_2= \text{row}_2 +\frac{3}{5}\text{row}_3$)
$$\begin{bmatrix}
2 & 1 & 1 &7 \\
0 & 1 & 0 & 7/5 \\
0 & 0 & -5 & -6
\end{bmatrix}$$
6. replacement 수행 ($\text{row}_1= \text{row}_1 +\frac{1}{5}\text{row}_3$)
$$\begin{bmatrix}
2 & 1 & 0 & 29/5 \\
0 & 1 & 0 & 7/5 \\
0 & 0 & -5 & -6
\end{bmatrix}$$
7. replacement 수행 ($\text{row}_1= \text{row}_1 -\text{row}_2$)
$$\begin{bmatrix}
2 & 0 & 0 & 22/5 \\
0 & 1 & 0 & 7/5 \\
0 & 0 & -5 & -6
\end{bmatrix}$$
8. scaling 수행 ($\text{row}_1= \frac{1}{2}\text{row}_1$)
$$\begin{bmatrix}
1 & 0 & 0 & 11/5 \\
0 & 1 & 0 & 7/5 \\
0 & 0 & -5 & -6
\end{bmatrix}$$
9. scaling 수행 ($\text{row}_3= \frac{-1}{5}\text{row}_3$)
$$\begin{bmatrix}
1 & 0 & 0 & 11/5 \\
0 & 1 & 0 & 7/5 \\
0 & 0 & 1 & 6/5
\end{bmatrix}$$
위에서 구한 matrix는 RREF이며, 쉽게 solution을 구할 수 있음.
$$
x_1 = 11/5, x_2=7/5, x_3=6/5 \blacksquare
$$
Gauss-Jordan Elimination Method의 사용처
- Solution 구하기.
- inverse matrix구하기.
Gauss-Jordan Elimination Method를 통해 solution 구할 수 있다는 애기는 coefficient matrix의 inverse를 구하는데에도 사용가능하다는 것을 의미한다. - rank계산 및 linear indepedent한 row vector 구하기
all-zero row의 경우 linearly dependent하므로 coefficient matrix의 rank 를 계산하는데 이용가능함.
추가로,
- REF를 구한 이후, Back substituion (후진 대입법)을 통해 해를 구하는 것이 Gauss Elimination Method (위의 예제에서 step4까지)이고,
- RREF까지 구하여 해를 구할 경우 Gauss-Jordan Elimination Method라고 함.
- REF는 element row operation들을 어떤 순서로 적용하느냐에 따라 다르므로 유일하게 결정되지 않으나, RREF는 유일(unique)하다. 때문에 library들에서 RREF는 함수로 제공되지만, REF는 아니다.
- 굳이 REF를 얻고 싶다면, LU decomposition 등으로 구할 수는 있음 (REF는 unique하진 않음을 명심.).
2022.09.02 - [Linear Algebra] - [LA] sympy로 Reduced Row Echelon Matrix 구하기.
[LA] sympy로 Reduced Row Echelon Matrix 구하기.
David C. Lay의 Linear Algebra에서 1.2장의 Example 3에 sympy적용. RREF는 unique하기 때문에 sympy에서 지원함. import numpy as np import sympy as sp # ---------------------------------- # colab에서 sympy의 값을 latex 지원하여 출
bme-g.tistory.com
참고로, Gauss Elimination은 B.C. 250년 당시 중국에서 사용되었고, 서구권에서는 19세기의 Gauss에 의해 사용되기 시작했다고 한다.
같이 보면 좋은 URLs
https://angeloyeo.github.io/2019/09/09/Gauss_Jordan.html
가우스-조던 행렬 소거법의 기하학적 의미 - 공돌이의 수학정리노트 (Angelo's Math Notes)
angeloyeo.github.io
2025.01.21 - [.../Linear Algebra] - [Summary] Linear Algebra (작성중)
[Summary] Linear Algebra (작성중)
ML 을 위해 Linear Algebra 공부시 참고할만한 책더보기전체적으로 공부를 한다면 다음을 권함.Linear Algebra and Its Application, 5th ed 이상, David C. Lay5th ed. 는 웹에서 쉽게 pdf도 구할 수 있음. 다음은 1~2개
dsaint31.tistory.com
'... > Linear Algebra' 카테고리의 다른 글
| [LA] Linear Transformation (1) | 2024.04.03 |
|---|---|
| [LA] Determinant (행렬식) (0) | 2024.04.03 |
| [LA] Row Operations and Row Equivalent (0) | 2024.02.17 |
| [LA] Pivot and Pivot Column (0) | 2024.02.17 |
| [LA] Existence and Uniqueness Theorem (1) | 2024.02.17 |