1. DTFT 의 한계와 DFT의 등장.
DTFT는
- time domain의 continuous signal $x(t)$를
- discrete signal $x[n]$으로 바꾼 경우에 대한
- Fourier Transform으로
CTFT에 time domain에서의 sampling을 고려한 확장이라고 볼 수 있다.
우선, DTFT의 공식은 다음과 같다.
$$\begin{aligned}X(e^{j\omega})&=\sum^\infty_{n=-\infty} x[n] e^{-j\omega n} & \text{DTFT} \\ x[n]&=\dfrac{1}{2\pi}\int_{<2\pi>} X(e^{j\omega }) e^{j\omega n }d\omega & \text{IDTFT} \end{aligned}$$
하지만 다음과 같은 한계를 가진다.
- $x[n]$에 대해 무한대 range에서 고려를 해야만 DTFT를 구할 수 있음.
- $x[n]$은 discrete이지만, $X(e^{j\omega})$는 continuous임 : computer로 처리할 경우 discrete로 바꾸어야한다.
- 신호와 스펙트럼 모두 discrete 해야 computer 에서 사용가능!
이같은 이유로 인해 제안된 것이 바로 Discrete Fourier Transform (DFT)임.
2. Discrete Fourier Transform (DFT)
DFT와 Inverse DFT는 다음과 같음:
$$\begin{aligned}X[k] &= \sum^{N-1}_{n=0} x[n] W^{kn}_N \\ x[n] &= \dfrac{1}{N}\sum^{N-1}_{k=0} X[k]W_N^{-kn} \\ W_N&=e^{-j\frac{2\pi}{N}}, \quad W_N \text{ is twiddle factor.}\end{aligned}$$
- Continuous Periodic Spectrum $X(e^{j\omega})$을 $N$ sampling하여
Discrete Periodic Spectrum $X[k]$얻음 - 그 결과로 이에 대응되는 Signal이 결국,
Discrete Non-periodic에서 Discrete Periodic Signal (아래그림에서 왼쪽 하단)이 됨.
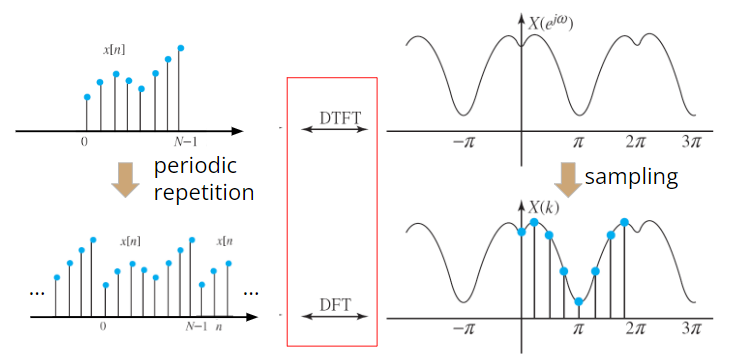
즉, DFT는 다음과 같이 볼 수 있음.
- Discreted aperiodic signal($N$ samples)의 Continuous Frequency Spectrum $X(e^{j\omega})$을
$N$ sampling한 것. - Discreted aperiodic signal($N$ samples)을 주기가 $N$인 주기 신호의 한 주기에 해당하는 것으로 취급
- 때문에 Frequency Spectrum도 최소한 $N$ 개 이상으로 sampling해야한다.
- 만약, time domain의 신호의 샘플 수 $N$보다 작은 수의 samples를 가지도록
Frequency spectrum이 sampling 될 경우,
time domain의 signal (위그림의 왼쪽 하단) 에서 aliasing(중첩)이 발생되어
IDFT를 해도 제대로 된 신호를 못 얻음.
신호를 측정하는 시간($T_\text{duration}$)이 고정된 경우, 원하는 주파수 유효 band-width에 맞춰 $N$이 결정됨.
2023.12.07 - [.../Signals and Systems] - [SS] DFT에서 Aliasing을 피하기 위한 N은?
[SS] DFT에서 Aliasing을 피하기 위한 N은?
1. Aliasing을 피하기 위한 적절한 샘플수가 필요한 이유Signal을 sampling할 경우,sample의 갯수 $N$를 제한 (= signal의 길이가 제한)할 경우,대응하는 spectrum에서 aliasing이 발생하게 됨(신호의 측정시간이
dsaint31.tistory.com
Frequency domain에서의 sampling은 frequncy resolution이라는 개념과 연결됨.
2022.11.25 - [.../Signals and Systems] - [SS] Resolution of DFT
[SS] Resolution of DFT
1. Picket Fence EffectDFT의 경우 spectrum도 discrete하게 존재하기 때문에 spectrum에서의 sampling interval(=실제 값을 가진 샘플의 간격)이 지나치게 넓을 경우, Picket Fence Effect로 인한 문제점 발생. (=너무 듬성
dsaint31.tistory.com
DTFT는 DTFS와 매우 유사하나, 다음과 같은 차이가 있음.
- DTFS : 1/N 이 분석식, 즉 Fourier Coefficient (푸리에 계수) 계산식에 붙음
- DFT : 1/N 이 합성식, 즉 IDFT 식에 붙음 (∵ $X(\omega)$의 샘플링 개념으로 유도)
3. DFT의 개념도
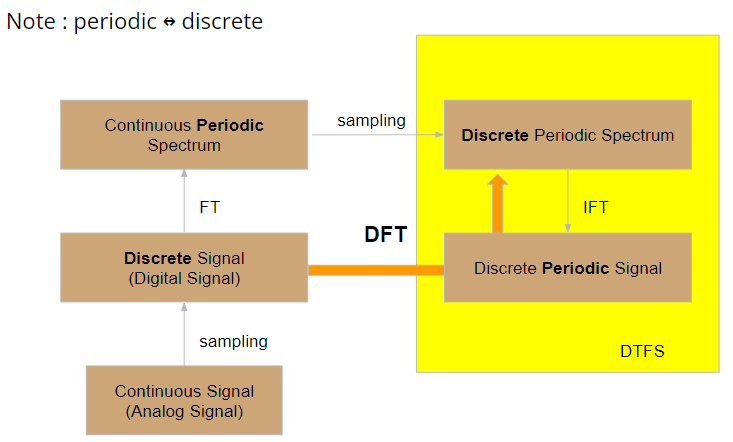
CTFS, CTFT, DTFS, DTFT는 FT의 종류 혹은 분류이나
DFT는 FT의 한 종류라기 보다는
단지 수치적으로 FT를 수행하기 위한 도구일 뿐 임.
4. Twiddle Factor (회전인자): $W_N$
$$ W_N = e^{-j\dfrac{2\pi}{N}} $$
$W_N^{kn}$은 복소평면의 단위원을 같은 크기의 각도로 $N$ 등분한 점에 해당함 : Complex Exponential 에 대한 간결한 표현.
- $W_N^{kn}$은 N을 주기로 하는 periodic function임 : $W_N^{kn+N}=W^{kn}_N$
- exponent에 마이너스 기호가 있기 때문에 clockwise 로 회전함.
- $W_N$이 한번 곱해질 때마다 clockwise로 정해진 각도만큼 회전
- $N$이 정해지면 미리 계산해놓을 수 있음.
다음은 $N=8$인 경우의 twiddle factor임.

5. Inverse DFT (IDFT) 구하기.
complex conjugate는 다음과 같은 성질을 가짐.
$$ (a^*)^* = a \\ (a+b)^* = a^* + b^* \\ (ab)^* = a^*b^*$$
위에서 첫번째 행의 등식으로, 다음이 성립함:
$$x[n] =\frac{1}{N} \sum^{N-1}_{k=0}X[k]W_N^{-kn}= (x^*[n])^*$$
complex conjugate의 성질(앞서 다룬 3가지 등식 중 2,3번째 행의 등식)에 의해 $x^*[n]$을 구하면 다음과 같음.
$$\begin{aligned}x^*[n] &= \left(\frac{1}{N} \sum^{N-1}_{k=0}X[k]W_N^{-kn}\right)^* \\ &= \color{green}{\frac{1}{N}}\color{black}{}\sum^{N-1}_{k=0}\color{blue}{X^*[k]}\color{black}{}W_N^{\color{red}{kn}}\end{aligned}$$
이는 DFT에서의 twiddle factor의 exponent $\color{red}{kn}$을 동일하게 가짐.
$$\text{DFT: }X[k] = \sum^{N-1}_{n=0} \color{blue}{x[n]}\color{black}{} W_N^{\color{red}{kn}}$$
- $x^*[n]$의 DFT와의 차이점은
- $\frac{1}{N}$을 곱해준 부분 (green으로 표기)과
- source function이 $x[n]$ 대신에 $X^*[k]$ 이라는 점 뿐임(blue로 표기)
이를 $x[n] = (x^*[n])^*$의 $x^*[n]$에 대입하면, 다음이 성립함.
$$x[n] = (x^*[n])^* = \frac{1}{N} \left(\sum^{N-1}_{k=0}X^*[k]W_N^{kn} \right)^*$$
이 경우 IDFT를 따로 구현하지 않고, DFT의 모듈을 사용할 수 있다.
즉, 다음의 순서로 IDFT를 구하면 됨.
1. $X[k]$의 imaginary part의 부호를 변경: $X^*[k]$를 구함
2. $X^*[k]$를 DFT 모듈에 입력하여 결과를 구함: $\sum^{N-1}_{k=0}X^*[k]W_N^{kn}$을 구함.
3. 2번 과정의 결과물을 complex conjugate를 구함: $\left( \frac{1}{N}\sum^{N-1}_{k=0}X^*[k]W_N^{kn} \right)^*$
4. 3번의 결과물을 $N$으로 나누어줌: $\frac{1}{N} \left( \sum^{N-1}_{k=0}X^*[k]W_N^{kn} \right)^*$
4번의 결과물이 곧 $x[n]$임.
같이 보면 좋은 자료들
[SS] Discrete Time Fourier Transform (DTFT) and Discrete Fourier Transform (DFT)
0. Pre-requirements2023.10.19 - [.../Signals and Systems] - [SS] Convolution with an shifted impulse [SS] Convolution with an shifted impulse0. shifted impulse와 convolution은 결국 shifting 연산임$t_0$로 shifting을 시킨 impulse function $\delta(
dsaint31.tistory.com
'... > Signals and Systems' 카테고리의 다른 글
| [SS] DFT에서 Aliasing을 피하기 위한 N은? (0) | 2023.12.07 |
|---|---|
| [SS] Fourier Analysis: 4가지 Fourier Transform 비교 (0) | 2023.12.07 |
| [SS] Discrete Time Fourier Transform (1) | 2023.12.03 |
| [SS] Discrete Sinusoidal Function : $2\pi$ 주기성 (1) | 2023.11.30 |
| [SS] Poles and Zeros: Impulse Response and Frequency Response (0) | 2023.11.16 |