Zero, Pole and ROC
2023.06.16 - [.../Signals and Systems] - [SS] z-Transform : Zero, Pole, and ROC
[SS] z-Transform : Zero, Pole, and ROC
z-Transform의 일반형은 다항식( polynomial)을 분자(numerator), 분모(denominator)로 가지는 분수 형태로 표현됨. $$ H(z)=\frac{P(z)}{Q(z)}=\frac{\displaystyle\sum^M_{m=0}b_m z^{-m}}{\displaystyle 1+\sum^N_{n=1}a_nz^{-n}} $$ 이 때, nu
dsaint31.tistory.com
Region of Convergence (ROC, 수렴영역)
z-Transform은 Laplace Transform의 discrete version이라고 볼 수 있기 때문에, 마찬가지로 ROC가 존재함.
(Unilateral z-Transform의 경우, ROC가 없이 사용가능하나, Bilateral z-Transform의 경우 반드시 기재가 되어야함.)
이후 살펴볼 대표적인 세 경우에서 ROC는 다음이 성립.
- Right-side Signal의 ROC는 "무한대"를 포함.
- Left-side Signal의 ROC는 $z=0$(origin, 원점)을 포함.
- Two-side Signal의 ROC는 존재한다면 Ring의 형태임.
Right-side Signal
예를 들어 다음 함수가 있다고 하자.
$$ x_R[n] = a^n u[n] , |a|<1$$
이 함수의 z-Transform 는 다음과 같음.
- Sol.
$$ \begin{align*} X_R(z) &= \sum_{n=0}^{\infty} a^n z^{-n} \\ &=\sum_{n=0}^{\infty} (az^{-1})^n,\quad |az^{-1}|<1 \rightarrow|z|>|a| \\ &=\frac{1}{1-az^{-1}}\end{align*} $$
right-sided 신호는 $\displaystyle X(z)=\sum^\infty_{n=0}x[n]z^{-n}$이기 때문에
$z^{-1}$의 기반의 등비급수임. 때문에 $z^{-1}$를 등비급수의 변수로 사용.
공비(common ratio ,$\frac{a}{z}$) 의 절대값이 1보다 작아야 수렴이 되며, 결국 $z$가 특정 범위에서만 선택가능함.
위의 경우의 ROC는 다음과 같음.
$$|z|>a$$
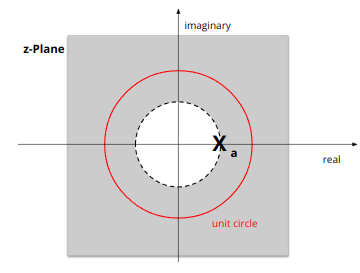
- Right-side Signal의 경우, ROC가 무한대를 포함.
- 위의 그림에서 점선(경계부분)은 ROC에 포함되지 않음.
- Pole (x기호로 표시됨)은 ROC에서 제외됨.
공비 :
2022.06.21 - [.../Signals and Systems] - [Math] Geometric Series (등비급수 or 기하급수)
[Math] Geometric Series (등비급수 or 기하급수)
Geometric Series의 Recurrence Formula (점화식) $a_n=ar^{n-1}$ 인 경우, 첫번째 term이 $a$이고 common ratio(공비)가 $r$임. 수식 : Series는 sequence의 합 Geometric Series $S_n$은 $a_1$부터 $a_n$까지의 합으로 다음과 같음. $$
dsaint31.tistory.com
Left-side Signal
예를 들어 다음 함수가 있다고 하자.
$$ x_L[n] = -a^n u[-n-1] , |a|<1$$
이 함수의 z-Transform 는 다음과 같음.
- Sol.
$$ \begin{align*} X_L(z) &= -\sum_{n=-\infty}^{\infty} a^n u[-n-1]z^{-n} \\ &= -\sum_{n=-\infty}^{\infty} a^n u[-(n+1)]z^{-n} \\&= -\sum_{n=-\infty}^{-1} a^n z^{-n} \\&=-\sum_{m=1}^{\infty} a^{-m}z^{m}, \quad m=-n \\ &=-\sum_{m=1}^{\infty} (a^{-1}z)^m,\quad |a^{-1}z|<1 \rightarrow|z|<|a| \\ &=\frac{-a^{-1}z}{1-a^{-1}z}\\&=\frac{z}{z-a} \\&=\frac{-\frac{z}{a}}{1-\frac{z}{a}} \end{align*} $$
left-sided signal의 경우 $\displaystyle X(z)=\sum^{-1}_{n=-\infty}x[n]z^{-n}$이므로
$z^{-(-1)}=z^1$ 등과 같이 $z$를 변수로 등비급수 전개를 해야함.
역시, 공비(common ratio, $\frac{z}{a}$) 의 절대값이 1보다 작아야 수렴이 되며, 결국 $z$가 특정 범위에서만 선택가능함.
위의 경우의 ROC는 다음과 같음.
$$|z|<a$$

- Left-side Signal의 경우, ROC가 $z=0$을 포함.
- 위의 그림에서 점선(경계부분)은 ROC에 포함되지 않음 (unit circle도 마찬가지).
- Pole (x기호로 표시됨)은 ROC에서 제외됨.
앞서 살펴본 Right-side Signal과 Left-side Signal은 분명 다른 signal이지만 같은 z-Transform을 가지게 됨.
때문에 이 둘의 구분을 위해서 ROC(수렴영역)이 반드시 기재되어야 함.
Two-side Signal
예를 들어 다음 함수가 있다고 하자.
$$ x[n] = a^n u[n]+a^{-n} u[-n-1] , |a|<1$$
- 앞서의 예제에서 right-sided signal은 동일함.
- 단, left-sided signal은 다름에 주의 (때문에 ROC도 달라짐)
이 함수의 z-Transform 는 다음과 같음.
- Sol.
$$ \begin{aligned} X(z) &= \sum_{n=-\infty}^{\infty} a^n u[n] z^{-n}+\sum_{n=-\infty}^{\infty} a^{-n} u[-n-1] z^{-n} \\&=\sum_{n=0}^{\infty} a^nz^{-n}+\sum^{-1}_{n=-\infty}a^{-n}z^{-n},\quad m=-1\\ &=\sum_{n=0}^{\infty} (az^{-1})^n + \sum_{m=1}^{\infty} (az)^m,\quad |az^{-1}|<1 ,|az|<1\rightarrow|a|<|z|<\frac{1}{|a|} \\ &= \frac{1}{1 - a z^{-1}} + \frac{a z}{1 - a z}. \\ & =\frac{(a-a^{-1})z}{(z-a)(z-a^{-1})} \end{aligned} $$
이 경우의 ROC는 다음과 같음.
$$a<|z|<\frac{1}{a}$$
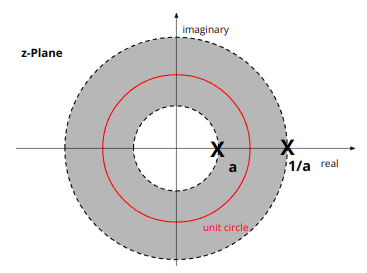
- Two-side Signal의 경우, ROC가 존재한다면 Ring형태임.
- 위의 그림에서 점선(경계부분)은 ROC에 포함되지 않음.
- Pole (x기호로 표시됨)은 ROC에서 제외됨.
같이보면 좋은 자료
2022.11.30 - [.../Signals and Systems] - [SS] z-Transform: Introduction
[SS] z-Transform: Introduction
1. z-Transform이란?Laplace Transform의 Discrete Version (or Generalization of DTFT)Continuous Time Signal과 System에서 Laplace Transform의 역할을Discrete Time Signal과 Discrete Time System에서 담당.수식적으로 보면, DTFT (Discrete Time
dsaint31.tistory.com
'... > Signals and Systems' 카테고리의 다른 글
| [SS] z-Transform : Transfer function (0) | 2023.06.16 |
|---|---|
| [SS] sinc function and sampling function (0) | 2022.12.09 |
| [SS] z-Transform: Introduction (1) | 2022.11.30 |
| [SS] Resolution of DFT (1) | 2022.11.25 |
| [SS] Discrete Convolution (Linear Discrete Convolution) (0) | 2022.11.22 |