필요조건, 충분조건, 필요충분조건
명제 (proposition)을 다룰 때 자주 나오는 애기임.
명제 (proposition)이란?
참(True)이나 거짓(False)를 판별할 수 있는 식(expression)이나 문장(statment).
conditional proposition(조건명제)가
필요조건, 충분조건, 및 필요충분조건 을 설명할 때 주로 사용되며
논리학 또는 기초 수학에서 흔히 보임:
premise(전제)와 conclusion(결론)의 두 집합간의 포함관계를 나타냄.
conditional proposition은 Implication(함의) 라고도 불리며,
premise가 참이면 conclusiont도 참이라는 논리적 관계로 if-then으로 자주 표기됨.
- $p$, premise(전제) 와 $q$, conclusion(결론) 으로 구성됨.
- $p$ 이면, $q$ 이다. (전형적인 조건명제)
주로 $p$와 $q$의 관계는 function이 그러했던 것처럼 집합(set)을 이용하여 자주 설명됨.
" $p$ 이면, $q$ 이다.
- 여기서 $p$와 $q$를 어떤 집합이라고 생각하자.
- 이 경우, 해당 명제가 참이 되기 위해선 $p$는 $q$에 포함되는 subset이 되어야 한다.
- 즉, $p \subset q$이 성립한다.
- 소크라테스($p$)는 인간($q$)이다 를 살펴보자.
- 소크라테스 는 인간에 포함된다.
- 단, $p$가 매우 클 경우, $q$와 같아질 수는 있으나, $q$를 넘어서는 크기의 집합이 될 수 없다: 크기는 포함의 관점에서의 크기임.
converse (역): q 이면 p이다.
contrapositive (대우): q가 아니면 p가 아니다.
inverse (부정): p 가 아니면 q가 아님.
필요조건 (necessary condition)
$q$ if $p$이다: $p \implies q$
premise $p$에 대해 conclusion $q$는 necessary condition임.
- $p$ 이면 $q$이다 라는 propostion에서, $q$는 $p$의 necessary condition이 된다.
- 집합으로 표현하면 $p \subset q$이다.
- 어떤 존재가 소크라테스가 이려면 (=$p$가 true이려면), 우선 해당 존재는 인간($q$가 true)이어야 한다
- $p$가 True가 되기 위해선 $q$가 일단 True여야 한다. 하지만, $q$가 True인 경우가 100% $p$가 True임을 보장하지는 않는다.
- "노력은 성공의 필요조건이다." 라는 말에는 $\text{성공} \rightarrow \text{노력}, \text{성공} \subset \text{노력}$을 의미한다.
- 즉, 성공한 사람은 모두 노력을 한 건 True (성공은 노력의 부분집합)이지만, 노력한 사람이 모두 성공한 건 아니라는 애기(성공 중 일부는 노력에 속하지 않음)가 된다.
충분조건 (sufficient condition)
$p$ only if $q$ 라고 표현된 경우, ($p \implies q$)
conclusion $q$에 대해 premise $p$는 sufficient condition임.
- $p$ 이면 $q$이다 라는 propostion에서, $p$는 $q$의 sufficient condition이 된다.
- 집합으로 표현하면 $p \subset q$이다.
- 어떤 존재가 소크라테스 라면 (=$p$가 true), 해당 존재는 100% 인간($q$가 true)임
- $p$가 True인 경우, $q$는 무조건 True임. 여야 한다. 하지만, $p$가 False인 경우에도 $q$가 True일 수 있음.
- 즉, sufficient condition이 true인 경우 무조건 true가 보장되고, false이더라도 true가 될 수 있음.
- "대학생은 학생의 충분조건이다." 라는 말에는 $\text{대학생} \rightarrow \text{학생}, \text{대학생} \subset \text{학생}$을 의미한다.
필요충분조건 necessary and sufficient condition
$p$ if and only if $q$ 라고 표현된 경우, premise $p$에 대해 conclusion $q$는 equivalent(동치)이다.
- "if and only if"는 줄여서 iif라고도 한다.
- $p \iff q$
Example
"optimal solution이면 Karush-Kuhn-Tucker condition을 만족한다."
$$\text{optimal solution} \implies \text{KKT condition}$$
여기서 optimal solution인 경우가 KKT conditon을 만족하는 경우에 포함된다.
- optimal solution에 대해 Karush-Kuhn-Tucker condtion을 만족하는 건 필요조건임.
- Karush-Kuhn-Tucker condition을 만족한다는 것에 대해 optimal solution은 충분조건임.
이는 Karush-Kuhn-Tucker conditino을 만족하는 경우, optimal solution일 수도 있고, 아닐 수도 있음을 의미.
하지만, optimal solution이면 반드시 Karush-Kuhn-Tucker condition을 만족한다.
유능한 공학자는 문제해결능력이 뛰어난 사람이다.
유능한 공학자라면 사람이다.
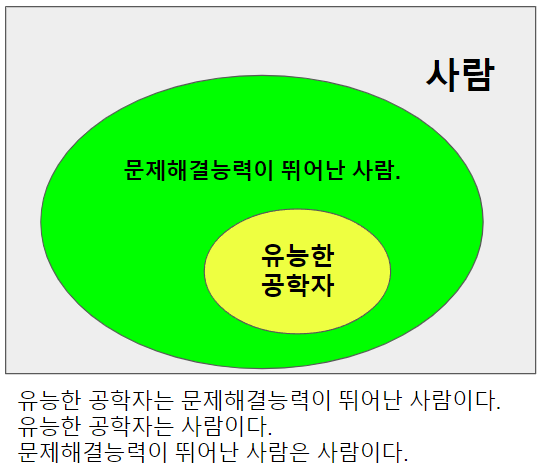
"유능한 공학자"는 "문제해결능력이 뛰어난 사람"에 대한 충분조건임.
"문제해결능력이 뛰어난 사람"은 "유능한 공학자"에 대한 필요조건임.
- 유능한 공학자는 100% 문제해결능력이 뛰어나다.
- 문제해결능력이 좋다고 해서 다 유능한 공학자라고 할 수 없다.
주기가 $2\pi$인 함수 $f(x)$는 다음의 식 $f(x)=f(x+2\pi)$를 만족한다.
이 경우, "주기가 $2\pi$인 함수 $f(x)$"는 "다음의 식 $f(x)=f(x+2\pi)$를 만족"에 대한 충분조건임.
"다음의 식 $f(x)=f(x+2\pi)$를 만족"하는 경우는 주기가 $4\pi$인 함수 $f(x)$도 만족하므로 더 큰 집합이다.
같이보면 좋은 자료들
2024.02.25 - [.../Math] - [Math] Class: set and proper class (클래스와 집합)
[Math] Class: set and proper class (클래스와 집합)
Class, Proper Class, and SetClass집합론 (Zermelo-Fraenkel set theory)에서Class는 구별가능한 수학적인 객체 (distinctive object)의 collection을 의미함.(Set은 collection of distinctive objects라고 말할 수 있으나, 여기에 well-
dsaint31.tistory.com
2023.05.17 - [.../Math] - [Math] Karush-Kuhn-Tucker Conditions (KKT Conditions)
[Math] Karush-Kuhn-Tucker Conditions (KKT Conditions)
KKT ConditionsKKT조건은inequality constraints을 가지는 constrained optimization problem의optimal solution이 만족해야하는 necessary condition들의 집합(4개의 necessary conditions)임.Lagransian multiplier (or dual variable)를 도입하
dsaint31.tistory.com
2022.09.01 - [.../Math] - [Math] Definition, Proposition, Axiom, and Theorem
[Math] Definition, Proposition, Axiom, and Theorem
Definition (정의)용어 등의 뜻을 명확하게 정한 것.용어 등에 대한 약속이므로 증명할 필요가 없음.단, well-defined가 되어야 함.Proposition (명제)참, 거짓을 분명하게 판단할 수 있는 "문장(statement)"이
dsaint31.tistory.com
'... > Math' 카테고리의 다른 글
| [ML] Likelihood (우도, 기대값) (0) | 2022.06.02 |
|---|---|
| [Math] Normal Equation : Vector derivative(Numerator Layout)를 이용한 유도 (0) | 2022.06.01 |
| [Math] Plane Equation : 평면의 방정식 (0) | 2022.05.19 |
| [Math] Orthogonal Projection (정사영) (0) | 2022.05.19 |
| [Math] Distance between Point and Plane : 점과 직선의 거리 (0) | 2022.05.19 |