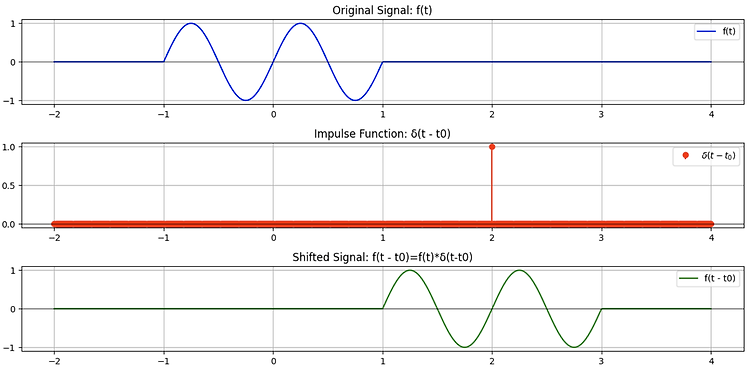
[SS] Convolution with an shifted impulse
·
.../Signals and Systems
0. shifted impulse와 convolution은 결국 shifting 연산임$t_0$로 shifting을 시킨 impulse function $\delta(t-t_0)$과의 convolution은결국 같은 $t_0$만큼 signal을 shifting하는 것으로 볼 수 있음.$$f(t)*\delta(t-t_0) = f(t-t_0)$$$*$ : convolution1. 증명$$ \begin{aligned} f(t)* g(t) &= \int^\infty_{-\infty} f(t-\color{red}{\tau}) g(\tau) d \tau \\ f(t)* \delta(t-t_0) &= \int^\infty_{-\infty} f(t-\tau) \delta(\tau - t_0) d \tau \\ &= \..


