Geometry

[Math] Geometry: Euclidean, Projective, Non-Euclidean

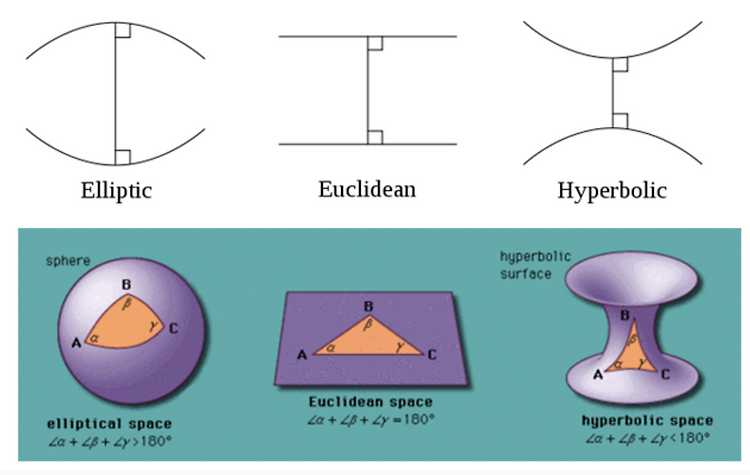
Euclidean Geometry(유클리드 기하학), Projective Geometry(사영 기하학), Non-Euclidean Geometry(비유클리드 기하학)기하학(Geometry)은 공간과 도형의 성질을 연구하는 수학의 한 분야임.기하학은 여러 종류가 있으며, 각각의 기하학은 서로 다른 공리와 개념에 기반함. 이 글에서는 Euclidean Geometry(유클리드 기하학), Projective Geometry(사영 기하학), Non-Euclidean Geometry(비유클리드 기하학)에 대해 소개함.일반적으로 Euclidean Geometry와 Non-Euclidean Geometry가 중요하나, Computer Vision 등에서 중요한 Projective Geometry를 같이 정리함.Euc..

[Math] Homogeneous Coordinate and Projective Geometry

Homogeneous Coordinates (동차 좌표)와 Projective Geometry (사영 기하학)1. 개요1-1. Homogeneous Coordinates의 정의와 특성Homogeneous Coordinates (동차 좌표)는 Euclidean Coordinates (유클리드 좌표) 시스템을 확장하여 Projective Geometry (사영 기하학)에서 사용되는 좌표 시스템임.이는 3차원 또는 2차원 Euclidean Space (유클리드 공간)의 점을 한 차원 더 높은 공간에서 표현하는 방법임.Projective Space $\mathbb{P}^2$는 평면(2차원)의 점을 homogeneous coordinates로 나타냄.$\mathbb{P}^2 = \mathbb{R}^3 - \mat..

[CV] Intersection and Ideal Point; Homogeneous Coordinate and Cross Product

Intersection and Ideal Point이 글에서는 homogeneous coordinates(동차 좌표)와 cross product(교차곱)을 이용하여 두 직선의 교점을 찾는 방법을 다룸.또한, 평행한 직선의 경우에 ideal point(이상점)이 나오는 경우도 다룸.두 직선의 교점을 구하는 방법단계별 설명1. Homogeneous Coordinates(동차 좌표):주어진 두 직선을 동차 좌표 $\mathbf{l}_1 = \begin{bmatrix}a_1 & b_1 & c_1\end{bmatrix}^\top$와 $\mathbf{l}_2 = \begin{bmatrix} a_2& b_2 & c_2\end{bmatrix}^\top$로 표현함.2. Cross Product Calculation(교차..