
삼각함수로 Fourier Series를 나타내면 다음의 장단점을 가짐:
- 모든 Fourier Series Coefficient가 실수임.
- 3종류를 구해야함: $a_0, a_k, b_k$ (이 단점으로 인해 주로 complex exponential로 표현한다)
Trigonometric Fourier series
Trigonometric function의 weighted sum (=linear combination)으로 periodic function을 나타낼 수 있음.
$$\tilde{x}(t)=a_0 + \displaystyle \sum^\infty_{k=1} \left[ a_k \cos k\Omega_0 t + b_k \sin k\Omega_0 t \right]$$
- $\Omega_0$ 는 fundamental frequency 로 주기 $T$와 다음의 관계를 가짐: $T=\frac{2\pi}{\Omega_0}$
다음은 Pulse wave(구형파) periodic signal을 Trigonometric Fourier series로 표현됨을 보여줌.
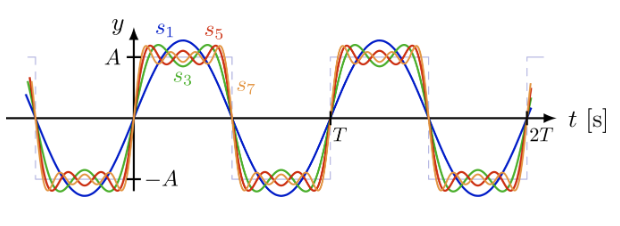
- $k=1,3,5,7$ 이며 $a_k=0$ 로 sin 성분만이 더해짐으로서 pulse wave가 됨을 보여줌.
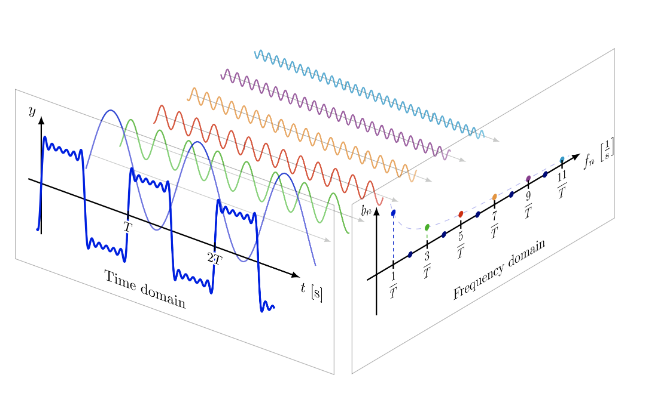
Fourier Series: Fourier coefficient구하기
rigonometric Fourier series의 weighted sum 에서의 각 coefficient 구하기.
cos 항에 대한 coefficient:
$$\begin{aligned}&\int_{t_0}^{t_0+T} \tilde{x}(t)\cos n\Omega_0 t dt \\
&= \int_{t_0}^{t_0+T} \left[ a_0 + \sum_{k=1}^{\infty} \left( a_k \cos k\Omega_0 t + b_k \sin k\Omega_0 t \right) \right] \cos n\Omega_0 t dt \\
&= a_0 \int_{t_0}^{t_0+T} \cos n\Omega_0 t dt + \sum_{k=1}^{\infty} a_k \left[ \int_{t_0}^{t_0+T} \cos k\Omega_0 t \cos n\Omega_0 t dt \right] + \sum_{k=1}^{\infty} b_k \left[ \int_{t_0}^{t_0+T} \sin k\Omega_0 t \cos n\Omega_0 t dt \right] \\
&= 0 + \sum_{k=1}^{\infty} a_k \left[ \int_{t_0}^{t_0+T} \cos k\Omega_0 t \cos n\Omega_0 t dt \right] + 0 \\
&= a_n \frac{T}{2}\end{aligned} \\
\therefore \quad a_n = \frac{2}{T} \int_{t_0}^{t_0+T} \tilde{x}(t)\cos n\Omega_0 t dt$$
sin 항에 대한 coefficient:
$$\begin{aligned}&\int_{t_0}^{t_0+T} \tilde{x}(t)\sin n\Omega_0 t dt \\
&= \int_{t_0}^{t_0+T} \left[ a_0 + \sum_{k=1}^{\infty} \left( a_k \cos k\Omega_0 t + b_k \sin k\Omega_0 t \right) \right] \sin n\Omega_0 t dt \\
&= a_0 \int_{t_0}^{t_0+T} \sin n\Omega_0 t dt + \sum_{k=1}^{\infty} a_k \left[ \int_{t_0}^{t_0+T} \cos k\Omega_0 t \sin n\Omega_0 t dt \right] + \sum_{k=1}^{\infty} b_k \left[ \int_{t_0}^{t_0+T} \sin k\Omega_0 t \sin n\Omega_0 t dt \right] \\
&= 0 + 0 + \sum_{k=1}^{\infty} b_k \left[ \int_{t_0}^{t_0+T} \sin k\Omega_0 t \sin n\Omega_0 t dt \right]\\
&= b_n \frac{T}{2}\end{aligned} \\
\therefore \quad b_n = \frac{2}{T} \int_{t_0}^{t_0+T} \tilde{x}(t)\sin n\Omega_0 t dt$$
bias 항:
$$a_0 =\frac{1}{T}\int^{t_0+T}_{t_0} x(t) dt$$
정리하면:
$$\begin{aligned}\tilde{x}(t)&=a_0 + \displaystyle \sum^\infty_{k=1} \left[ a_k \cos k\Omega_0 t + b_k \sin k\Omega_0 t \right], \quad T=\frac{2\pi}{\Omega_0} \\ \quad \\ a_0 &=\frac{1}{T}\int^{t_0+T}_{t_0} x(t) dt \\a_n &= \frac{2}{T} \int_{t_0}^{t_0+T} \tilde{x}(t)\cos n\Omega_0 t dt \\ b_n &= \frac{2}{T} \int_{t_0}^{t_0+T} \tilde{x}(t)\sin n\Omega_0 t dt\end{aligned}$$
예제:
다음 Pulse Wave에서 Fourier Series Coefficient를 $k=0,1,2,3$까지 구하라.

\begin{align*} b_{1} &= \frac{2}{T} \int_{0}^{2\pi} x(t) \sin t dt = \frac{1}{\pi} \int_{0}^{\pi} \sin t \, dt - \frac{1}{\pi} \int_{\pi}^{2\pi} \sin t dt \\ &= \frac{1}{\pi} \left\{ \big[-\cos t \big]_{0}^{\pi} + \big[ \cos t \big]_{\pi}^{2\pi} \right\} \\ &= \frac{1}{\pi} \{ 1 - (-1) + 1 - (-1) \} &= \frac{4}{\pi} \approx 1.273 \\ \quad \\ b_{3} &= \frac{2}{T} \int_{0}^{2\pi} x(t) \sin 3t dt = \frac{1}{\pi} \left\{ \int_{0}^{\pi} \sin 3t \, dt - \int_{\pi}^{2\pi} \sin 3t dt \right\} \\ &= \frac{1}{\pi} \left\{ \left[ \frac{-\cos 3t}{3} \right]_{0}^{\pi} + \left[ \frac{\cos 3t}{3} \right]_{\pi}^{2\pi} \right\} \\ &= \frac{1}{3\pi} \{ 1 - (-1) + 1 - (-1) \} &= \frac{4}{3\pi} \approx 0.424 \end{align*}
'... > Signals and Systems' 카테고리의 다른 글
| Parseval's Theorem (0) | 2025.10.15 |
|---|---|
| Complex Exponential Fourier Series (0) | 2025.10.01 |
| Unit Pulse Signal (Box Signal, Rect Signal) (3) | 2025.07.29 |
| Discrete Unit Step Function (1) | 2025.07.29 |
| Discrete Unit Impulse Signal (Kronecker Delta Function) (2) | 2025.07.29 |