Normal Distirbution
Gaussian Distribution, Laplace-Gaussian Distribution 라고도 불림.
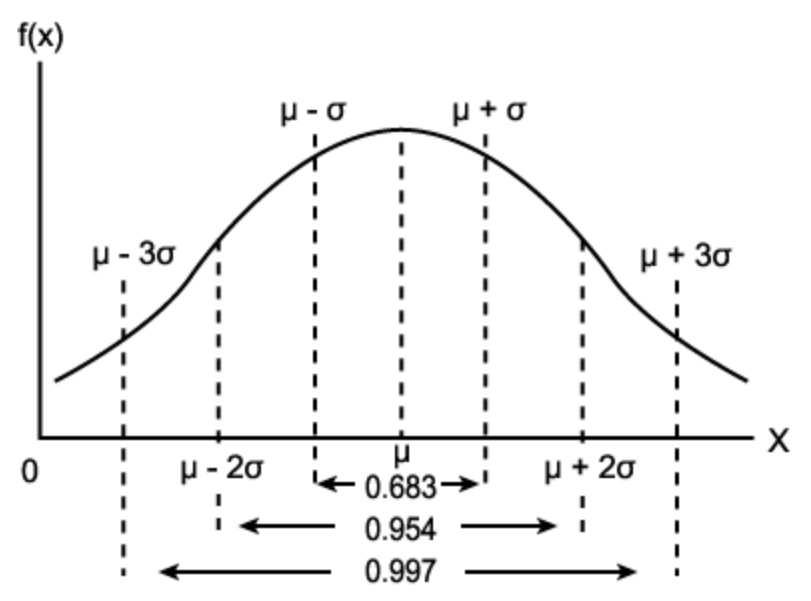
정의
PDF는 다음과 같음.
$$f(X)=\frac{1}{\sigma\sqrt{2\pi}}(e)^{-\frac{(X-\mu)^2}{2\sigma^2}}$$
- $\mu$ : mean
- $\sigma$ : standard deviation
PDF 이므로 probability를 다 더한 적분값은 1이 됨.
$\mu$와 $\sigma$가 parameter인데, 이들이 0과 1인 경우 standard normal distribution (표준정규분포)라고 불림.
일반 normal distribution에 z-Transform을 수행하면 standard normal distribution이 된다.
특징
Normal distribution 특징
- Independent value, Abscissa 는 실숫값을 취하며 ($-\infty,+\infty)$.
- mean(평균값) 부근의 확률밀도가 큼.
- mean에서 멀어질수록 확률밀도가 작음.
- 확률밀도가 mean을 중심으로 symmetric.
역사
de Moivre (드 므와브리)에 의해 1773년 binomial distribution의 근사로서 Normal distribution이 연구되었고,
Pierre Simmon Laplace에 의해 정확한 식이 정의되었음.
그후 Carl Friedrich Gauss에 의해 오늘날 사용되는 일반적인 식으로 정리됨.
Laplace와 Gauss 는 (천문)관측에서의
측정치의 error distribution의 연구에서 Normal distribution을 사용했기 때문에
"Normal law of error"라고도 불림.
Normal distribution 은 측정값에서
mean 주변의 variablity를 잘 설명함.
Francis Galton 등의 공헌과 Central Limit Theorem 덕분에
Normal distribution은 측정값들에 기반한 연구들에서 가장 널리 사용되는 확률분포 로 자리잡음.
- 대부분의 통계처리에서 dependent variable의 population이 normal distribution을 따른다고 가정한다.
- normal distribution을 따른다고 가정할 경우, 수많은 연구들 덕분에 inference를 위한 다양한 방법들이 존재함.
- Cntral Limit Theorem에 의해 population이 normal distribution이 아니더라도
이들의 측정치로 얻어진 sampling distribution은 ideal인 경우 normal distribution이라고 볼 수 있음.
2022.03.31 - [.../Math] - [Statistics] Central Limit Theorem
[Statistics] Central Limit Theorem
Central Limit Theorem (중심극한정리) mean의 sampling distribution의 다음과 같은 속성을 기술하는 Theorem. population이 무엇이든지 간에 sample size ($N$, 1개의 sample의 element의 수)가 충분히 크다(흔히 30 or 40이상)
dsaint31.tistory.com
다른 확률분포들과의 관계
binormial distribution에서 시행횟수 n을 무한대로 보내고, 성공확률 p를 0과 1에서 적절히 멀어지게 잡을 경우 normal distribution이 됨.
Poisson distribution의 경우엔 mean인 $\lambda$의 크기를 증가시킬 경우, normal distribution이 됨.
skewed to positive 의 경우 $\log$ 처리를, skewed to negative 인 경우엔 square처리 (cube 나 그 이상의 exponentiation)를 사용하여 normal distribution과 같이 symmetric shape가 되도록해줌.

Python code for Gaussian distribution
평균이 0이고 표준편차가 1인 standard normal distribution을 그려주는 code.
import matplotlib.pyplot as plt
import numpy as np
import scipy.stats
x = np.arange(-5,5,0.1)
mu = 0.
sigma = 1. # standard deviation
y = scipy.stats.norm.pdf(x=x, loc=mu, scale = sigma)
plt.plot(x,y, color='blue')
plt.show()

'... > Math' 카테고리의 다른 글
| [math] Factorial(계승), Permutation (순열) & Combination (조합) (1) | 2024.02.04 |
|---|---|
| [Math] Cartesian Product (or Descartes Product, Product Set) (0) | 2024.02.04 |
| [Math] Euler’s Constant (자연상수, 오일러 상수) (0) | 2023.10.25 |
| [Math] Poisson Distribution (포아송분포) (1) | 2023.10.25 |
| [Math] Derivative of Logistic Function (0) | 2023.09.25 |