Geometric Series의 Recurrence Formula (점화식)
$a_n=ar^{n-1}$ 인 경우,
- 첫번째 term이 $a$이고
- common ratio(공비)가 $r$임.
점화식(recurrence relation, recursion, recurrence formula)은
현재 값이 이전 값(들)의 함수로 정의되는 모든 관계식을 가리킴.
수식 : Series는 sequence의 합
Geometric Series $S_n$은 $a_1$부터 $a_n$까지의 합으로 다음과 같음.
$$\begin{aligned}S_n&=a+ar^1+ar^2\cdots+a^{n-1}\\&=\sum^n_{k=1}ar^{k-1}\end{aligned}$$
1. common ratio $r$이 1이 아닌 경우 다음이 성립.
$$S_n = \frac{a(1-r^n)}{(1-r)}$$
유도과정은 다음과 같음.
$$\begin{aligned}S_n&=a+ar+ar^2+\cdots+ar^{n-1}\\rS_n&=ar+ar^2+\cdots+ar^{n-1}+ar^{n}\\S_n-rS_n&=a-ar^n\\(1-r)S_n&=a(1-r^n)\quad,\text{where } r\ne1 \\ \\S_n&=\frac{a(1-r^n)}{1-r} \end{aligned}$$
2. common ratio $r =1$인 경우는
$$S_n=na$$
가 됨.
2023.07.21 - [.../Math] - [Math] Sequence (수열) and Series (급수)
[Math] Sequence (수열) and Series (급수)
Sequence수열, 열 이라고 불림.numbers나 objects 들이 순서를 가지고(ordered) 나열된 것을 가리킴.order(순서)가 의미를 가지며, (order가 다르기 때문에 )중복이 허용이 된다.대표적인 예로 arithmetic sequence(
dsaint31.tistory.com
신호처리와 Geometric series
신호처리에서는 common ratio의 절대값이 1보다 작은 경우의 infinite geometric series가 많이 사용됨.
Infinite geometric series (with $|r|<1$)는 다음과 같음.
$$\sum^\infty_{t=0}ar^t=\underset{n\to\infty}{\lim}\sum^n_{t=0}ar^t=\underset{n\to\infty}{\lim}\frac{a(1-r^n)}{1-r}=\dfrac{a}{1-r}\quad,\text{where }|r|<1$$
읽어보면 좋은 자료
수열과 급수의 기초 (Sequence, Series)
이제부터 미적분학의 급수에 관한 주제를 다루게 될 것입니다. 고등학교에서 배우는 수열과 급수와는 다르게, 대학 미적분학에서 급수는 대부분 무한급수를 다루게 되고, 일반적인 수열이나
gosamy.tistory.com
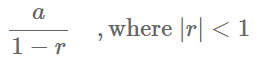
'... > Signals and Systems' 카테고리의 다른 글
| [SS] Impulse Function (Dirac Delta Function) (0) | 2022.08.29 |
|---|---|
| [SS] Example : Sampling function and Sinc function. (0) | 2022.08.29 |
| [SS] FT of phase shifted sinusoid! (0) | 2021.12.07 |
| [SS] Partial Fraction Decomposition (부분분수분해) (0) | 2021.11.11 |
| [SS] Impulse Train 의 FT 구하기. (0) | 2021.10.28 |