$f(t)=A\sin (\omega_0 t-\theta)$ 에 대한 Fourier Transform 구하기.
1. phase가 없는 경우를 구하고
$\mathscr{F}[\sin \omega_0 t]$ 는 다음과 같음.
$$\begin{aligned}\mathscr{F}[\sin \omega_0 t] & = \int_{-\infty}^{\infty} \sin \omega_0 t e^{-j\Omega t} dt\\
&= \int_{-\infty}^{\infty} \frac{e^{j\omega_0 t}-e^{-j\omega_0 t}}{2j} e^{-j\Omega t} dt \\
&= \frac{1}{2j} \left\{ \int_{-\infty}^{\infty} e^{j\omega_0 t} e^{-j\Omega t} dt - \int_{-\infty}^{\infty} e^{-j\omega_0 t} e^{-j\Omega t} dt \right\} \\
&= \frac{-j}{2}\left\{ 2\pi \delta(\Omega -\omega_0)- 2\pi \delta(\Omega+\omega_0)\right\} \\
&= -j\pi \delta(\Omega -\omega_0) +j\pi \delta(\Omega+\omega_0)
\end{aligned}$$
2. Frequency domain에서 phase shift는 Time domain에서의 time shift.
한쪽 domain에서의 (linear) phase shift는 다른 domain에서의 time shift에 해당함.
다음은 time domain에서 time shift ($t_0$만큼 delay)가 frequency domain에서 phse shift로 이어짐을 보여줌.
$$\begin{aligned}
\mathscr{F}[ f(t-t_0) ] &= \int_{-\infty}^\infty f(t+t_0)e^{-j\Omega t} dt \\
&=e^{-j\Omega t_0}\int_{-\infty}^\infty f(t)e^{-j\Omega t} dt \\
&=\bbox[5px,border:2px solid #FF0000]{e^{-j\Omega t_0}\mathscr{F} [ f(t) ]}
\end{aligned}$$
3. 최종풀이.
1에서 구한 식에 2번의 phase shift를 반영하면 됨.
$f(t)=A\sin (\omega_0 t-\theta)=A\sin (\omega_0 (t-\frac{\theta}{\omega_0}))$ 이므로, 이에 대한 FT는 다음과 같음.
$$\begin{aligned} \mathscr{F}[ A \sin (\omega_0 t-\theta)] &= \mathscr{F} [ A\sin (\omega_0 (t-\frac{\theta}{\omega_0}))] \\
&= e^{-j\Omega t_0} \left\{-j\pi \delta(\Omega -\omega_0) + j\pi \delta(\Omega+\omega_0) \right\} \\
&= e^{-j\Omega \frac{\theta}{\omega_0}} \left\{-j\pi \delta(\Omega -\omega_0) + j\pi \delta(\Omega+\omega_0) \right\} \\
&= e^{-j\Omega \frac{\theta}{\omega_0}} \left\{-j\pi \delta(\Omega -\omega_0) \right \}+ e^{-j\Omega \frac{\theta}{\omega_0}} \left\{j\pi \delta(\Omega+\omega_0) \right\} \\
&= e^{-j\omega_0 \frac{\theta}{\omega_0}} \left\{-j\pi \delta(\Omega -\omega_0) \right \}+ e^{-j(-\omega_0) \frac{\theta}{\omega_0}} \left\{j\pi \delta(\Omega+\omega_0) \right\} \\
&= e^{-j\theta} \left\{-j\pi \delta(\Omega -\omega_0) \right \}+ e^{j\theta} \left\{j\pi \delta(\Omega+\omega_0) \right\} \\
\end{aligned}$$
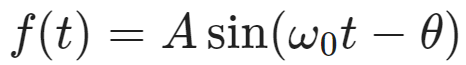
$cos$에 대한 경우는 다음의 동영상을 참고할 것.
'... > Signals and Systems' 카테고리의 다른 글
| [SS] Impulse Function (Dirac Delta Function) (0) | 2022.08.29 |
|---|---|
| [SS] Example : Sampling function and Sinc function. (0) | 2022.08.29 |
| [Math] Geometric Series (등비급수 or 기하급수) (0) | 2022.06.21 |
| [SS] Partial Fraction Decomposition (부분분수분해) (0) | 2021.11.11 |
| [SS] Impulse Train 의 FT 구하기. (0) | 2021.10.28 |